题目内容
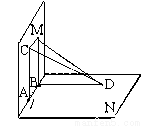
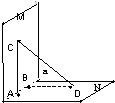如图所示，平面M、N互相垂直，棱a上有两点A、B，AC?M，BD?N，且AC⊥a，BD⊥a，AB=12cm，AC=3cm，BD=4cm，则CD=13cm
13cm
．分析：连接AD后，根据已知中平面M、N互相垂直，我们易得△ABC，△BCD均为直角三角形，根据勾股定理我们易求出BC的长，进而求出CD的长．
解答：解：连接AD
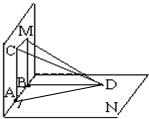
∵平面M、N互相垂直，BD⊥a，
∴BD⊥平面M，∴BD⊥BC
∵AB=12cm，AC=3cm，AB⊥AC，∴BC=
cm，
又∵BD=4cm，BD⊥BC
∴CD=13cm
故答案为：13cm．
∵平面M、N互相垂直，BD⊥a，
∴BD⊥平面M，∴BD⊥BC
∵AB=12cm，AC=3cm，AB⊥AC，∴BC=
| 153 |
又∵BD=4cm，BD⊥BC
∴CD=13cm
故答案为：13cm．
点评：本题考查的知识点是空间点到点之间的距离，其中根据面面垂直及线面垂直的性质得到△ABC，△ACD均为直角三角形，是解答本题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
11、如图所示，平面M、N互相垂直，棱l上有两点A、B，AC?M，BD?N，且AC⊥l，AB=8cm，AC=6cm，BD=24cm，则CD=
如图所示，平面M、N互相垂直，棱l上有两点A、B，AC?M，BD?N，且AC⊥l，BD⊥l，AB=3cm，AC=5cm，BD=4cm，则CD与平面N所成角的大小为
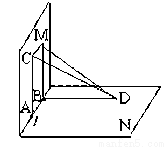
M，BD
M，BD