题目内容
设f(x)是以2为周期的奇函数,且f(- )=3,若sinα=
)=3,若sinα= ,则f(4cos2α)= ( )
,则f(4cos2α)= ( )
| A.-3 | B.3 | C.- | D. |
A
解析试题分析:∵sinα= ,∴cos2α=1-2sin2α=
,∴cos2α=1-2sin2α= ,∴f(4cos2α)=f(
,∴f(4cos2α)=f(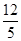 ),又函数f(x)是以2为周期的奇函数,∵f(-
),又函数f(x)是以2为周期的奇函数,∵f(- )=3,∴f(
)=3,∴f( )=-3,则f(
)=-3,则f(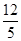 )=f(2+
)=f(2+ )=f(
)=f( )=-3.故选A
)=-3.故选A
考点:本题考查了二倍角公式及周期性
点评:此类问题为基础题,其中根据已知函数的周期性与奇偶性,寻找已知与求知函数值之间的关系是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 、
、 是方程
是方程 的两根,且
的两根,且 ,则
,则 ( )
( )
A. 或 或 | B. 或 或 | C. | D. |
已知 则
则 ( )
( )
A. | B. | C. | D. |
设 都是锐角,且
都是锐角,且 ,
, ,则
,则 =( )
=( )
A. | B. | C. 或 或 | D.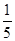 或 或 |
若 是
是 的内角,当
的内角,当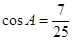 ,则
,则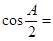
A. | B. | C. | D.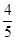 |
 等于( )
等于( )
| A.sin2-cos2 | B.cos2-sin2 | C.±(sin2-cos2) | D.sin2+cos2 |
已知 ,且
,且 ,则
,则 的值为
的值为
A. | B. | C. | D. |
求值 ( )
( )
A.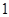 | B. | C. | D.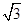 |
化简 的值为 ( )
的值为 ( )
| A.0 | B.- | C.2 | D. |