题目内容
用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并指出其定义域.?
解:由题意知,此框架围成的面积是由一个矩形和一个半圆组成的图形的面积,而矩形的长AB=2x,宽为a,则有2x+![]() -
-![]() x-x.?
x-x.?
半圆的直径为2x,半径为x.所以y=![]() x2+(
x2+(![]() -
-![]() x-x)·2x=-(2+
x-x)·2x=-(2+![]() )x2+lx.?
)x2+lx.?
根据实际意义知![]() -
-![]() x-x>0.因x>0,解得0<x<
x-x>0.因x>0,解得0<x<![]() ,即函数y=-(2+
,即函数y=-(2+![]() )x2+lx的定义域是{x|0<x<
)x2+lx的定义域是{x|0<x<![]() }.?
}.?
点评:求函数的定义域,如果是实际问题,除应考虑解析式本身有定义外,还应考虑实际问题有意义,如本题注意到矩形的长2x宽a必须满足2x>0和a>0,即l-πx-2x>0.

练习册系列答案
相关题目
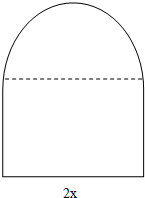 用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并写出其定义域.
用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并写出其定义域.
