题目内容
已知A、B、P是直线l上三个相异的点,平面内的点O∉l,若正实数x、y满足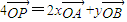 ,则
,则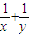 的最小值为 .
的最小值为 .
【答案】分析:由题意可得,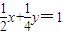 ,而
,而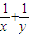 =(
=(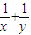 )(
)(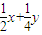 ),展开利用基本不等式即可求解
),展开利用基本不等式即可求解
解答:解:A、B、P是直线l上三个点,且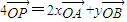 ,
,
即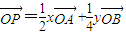
∴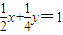
∴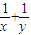 =(
=(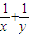 )(
)(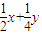 )
)
=
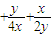
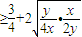 =
=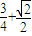
当且仅当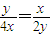 即y=
即y=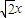
此时x=4-2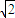 ,y=4
,y=4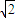 -4时取等号
-4时取等号
故答案为: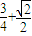
点评:本题主要考查了向量的共线定理的应用,基本不等式求解最值的应用,解题的关键是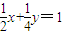
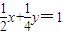 ,而
,而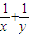 =(
=(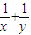 )(
)(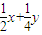 ),展开利用基本不等式即可求解
),展开利用基本不等式即可求解解答:解:A、B、P是直线l上三个点,且
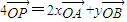 ,
,即
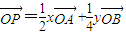
∴
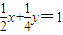
∴
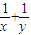 =(
=(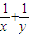 )(
)(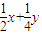 )
)=

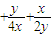
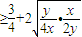 =
=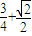
当且仅当
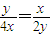 即y=
即y=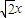
此时x=4-2
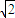 ,y=4
,y=4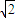 -4时取等号
-4时取等号故答案为:
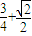
点评:本题主要考查了向量的共线定理的应用,基本不等式求解最值的应用,解题的关键是
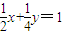

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目