题目内容
已知函数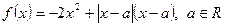 。
。
(I)当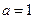 时,解不等式
时,解不等式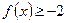 ;
;
(II)求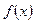 的最大值。
的最大值。
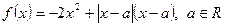 。
。(I)当
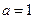 时,解不等式
时,解不等式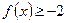 ;
;(II)求
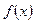 的最大值。
的最大值。解:(I)当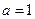 时,
时,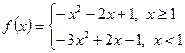
原不等式等价于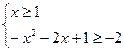 ,或
,或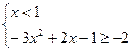
故原不等式的解集为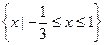 ;
;
(II)∵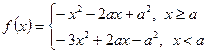
即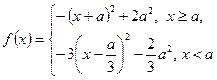
①当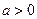 时,在
时,在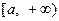 上
上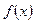 单减,最大值为
单减,最大值为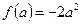 ,
,
在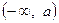 上
上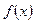 先增后减,最大值为
先增后减,最大值为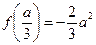 ,
,
此时,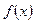 在
在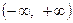 上最大值为
上最大值为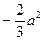 ;
;
②当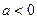 时,在
时,在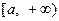 上
上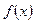 先增后减,最大值为
先增后减,最大值为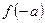
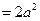 ,
,
在 上
上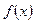 单增,最大值为
单增,最大值为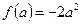 ,
,
此时,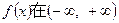 上最大值为
上最大值为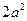
③当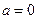 时,
时,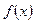 在
在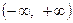 上最大值为0。
上最大值为0。
综上,当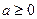 时,
时,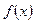 最大值为
最大值为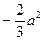 ;当
;当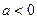 时,
时,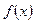 最大值为
最大值为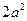 。
。
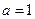 时,
时,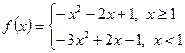
原不等式等价于
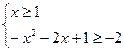 ,或
,或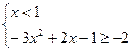
故原不等式的解集为
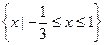 ;
;(II)∵
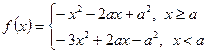
即
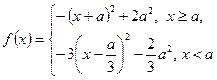
①当
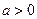 时,在
时,在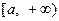 上
上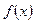 单减,最大值为
单减,最大值为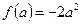 ,
,在
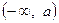 上
上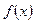 先增后减,最大值为
先增后减,最大值为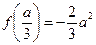 ,
,此时,
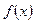 在
在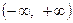 上最大值为
上最大值为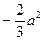 ;
;②当
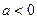 时,在
时,在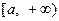 上
上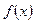 先增后减,最大值为
先增后减,最大值为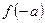
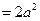 ,
,在
 上
上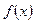 单增,最大值为
单增,最大值为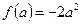 ,
,此时,
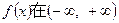 上最大值为
上最大值为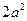
③当
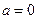 时,
时,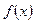 在
在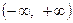 上最大值为0。
上最大值为0。综上,当
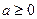 时,
时,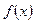 最大值为
最大值为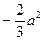 ;当
;当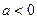 时,
时,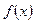 最大值为
最大值为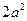 。
。略

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
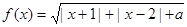 。
。 时,求函数
时,求函数 的定义域;
的定义域; ,试求
,试求 的取值范围.
的取值范围.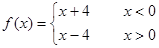 ,则
,则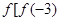 ]的值为 ( )
]的值为 ( ) 为奇函数,
为奇函数,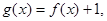 则
则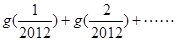
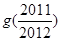 =( )
=( )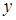 是一腰长
是一腰长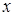 的函数,则
的函数,则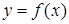 等于( )
等于( ) 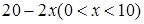 B
B 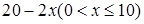
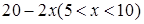 D
D 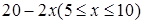
 ,则
,则 在
在 处的切线斜率为( )
处的切线斜率为( ) 


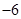
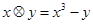 , 则
, 则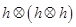 等于
等于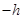
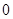
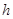
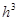
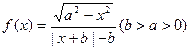 为奇函数;
为奇函数;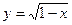 的值域为
的值域为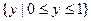 ;
;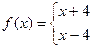
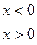 ,则
,则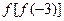 的值为_______________
的值为_______________