题目内容
设直线(A)1 (B)2 (C)3 (D)4
B
解析:由已知求得l′:2x+y-2=0与椭圆两交点分别为长、短轴端点,其中A(0,2),B(1,0),∴|AB|=![]() .∴顶点P到底边AB的距离h=
.∴顶点P到底边AB的距离h=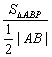 =
=![]() .
.
设与直线l′平行且距离为![]() 的直线l″:2x+y+C=0(C≠-2).
的直线l″:2x+y+C=0(C≠-2).
由两平行直线间距离公式,得d=![]() =
=![]() =
=![]() .
.
∴C=-1或C=-3.
两平行线为2x+y-1=0,2x+y-3=0.
联立①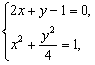
②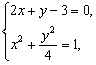
对于方程组①,Δ1>0,则直线与椭圆必有两个满足题意的P点.
对于方程组②,Δ2<0,直线与椭圆无交点.
综合知,满足题意的点P有2个,如下图.
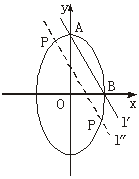

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为
的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为 的点M的个数为
的点M的个数为
 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 的交点为
的交点为 ,
, 两点,点
两点,点 是椭圆上的动点,则使
是椭圆上的动点,则使 的面积为
的面积为 的点
的点 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 的交点为A、B、,点
的交点为A、B、,点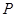 为椭圆上的动点,则使
为椭圆上的动点,则使 的面积为
的面积为 的点
的点