题目内容
某商场为促销设计两套方案:(1)全场九折;(2)购物100元摸彩球打折,8个红色和8个绿色的玻璃球放在一个盒子里,顾客任意摸出8个球,仅有抽出的红球、绿球个数相等时不打折,两者相差一个时打9折,两者相差2个或2个以上时打8折,问商场应选择哪种方案更有利可图?
选择第二种方案,更有利可图
应选第二种方案.此题实质上是计算满足一定条件的组合.其中摸出的红球、绿球相
等,可分两步完成,即第一步:在8个红球中取出4个红球;第二步在8个绿球中取4个绿球.所以有 ="4" 900种.
="4" 900种.
类似地同求得取5个红球和3个绿球的组合数为 ·
·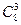 ="3" 136;
="3" 136;
取3个红球,5个绿球的组合数为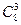
 ="3" 136;
="3" 136;
取6个红球2个绿球或2个红球6个绿球的组合数都为 ·
· =784;
=784;
取7红球1个绿球或1个红球7个绿球的组合数都为 =64;
=64;
取8个红球或8个绿球的组合数均为1.
从而不打折的有4 900种选法,打9折的有2×3 136="6" 272种选法,打8折的有2×(1+64+78
4)="1" 698种,不打折的比例超过打8折的比例,并且还必须购满100元才能打折,因此商场选择第二种方案,更有利可图.
等,可分两步完成,即第一步:在8个红球中取出4个红球;第二步在8个绿球中取4个绿球.所以有
 ="4" 900种.
="4" 900种.类似地同求得取5个红球和3个绿球的组合数为
 ·
·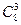 ="3" 136;
="3" 136;取3个红球,5个绿球的组合数为
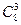
 ="3" 136;
="3" 136;取6个红球2个绿球或2个红球6个绿球的组合数都为
 ·
· =784;
=784;取7红球1个绿球或1个红球7个绿球的组合数都为
 =64;
=64;取8个红球或8个绿球的组合数均为1.
从而不打折的有4 900种选法,打9折的有2×3 136="6" 272种选法,打8折的有2×(1+64+78
4)="1" 698种,不打折的比例超过打8折的比例,并且还必须购满100元才能打折,因此商场选择第二种方案,更有利可图.

练习册系列答案
相关题目
 的展开式中
的展开式中 的系数为 .(用数字作答)
的系数为 .(用数字作答)