题目内容
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F. 现在老王决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且已经求得 .
.
(1)请你帮老王算出a,b,φ,并回答股价什么时候见顶(即求F点的横坐标);
(2)老王如能在今天以D点处的价格买入该股票5000股,到见顶处F点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
 .
.(1)请你帮老王算出a,b,φ,并回答股价什么时候见顶(即求F点的横坐标);
(2)老王如能在今天以D点处的价格买入该股票5000股,到见顶处F点的价格全部卖出,不计其它费用,这次操作他能赚多少元?

解:(1)∵C,D关于直线l对称∴C点坐标为(2×34﹣44,16),即(24,16),
把A、B、C的坐标代入解析式,得
 .
.
②﹣①得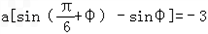 ,
,
③﹣①得 ,
,
∴
∴ .
.
∴ ,
,
∴
∵0<φ<π
∴ ,
,
代入②得b=19,
再由①得a=6.
∴a=6,b=19, .
.
于是,ABC段的解析式为 ,
,
由对称性得,DEF段的解析式为 .
.
∴ ,解得xF=92.
,解得xF=92.
∴当x=92时,股价见顶.
(2)由(1)可知,yF=6+19=25,
故这次操作老王能赚5000×(25﹣16)=45000元.

把A、B、C的坐标代入解析式,得
 .
.②﹣①得
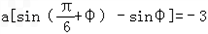 ,
,③﹣①得
 ,
,∴

∴
 .
.∴
 ,
,∴

∵0<φ<π
∴
 ,
,代入②得b=19,
再由①得a=6.
∴a=6,b=19,
 .
.于是,ABC段的解析式为
 ,
,由对称性得,DEF段的解析式为
 .
.∴
 ,解得xF=92.
,解得xF=92.∴当x=92时,股价见顶.
(2)由(1)可知,yF=6+19=25,
故这次操作老王能赚5000×(25﹣16)=45000元.


练习册系列答案
相关题目
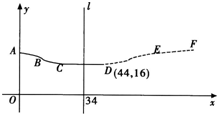 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F. ,
, 

 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 来描述,从
来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 :
: 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 段是股价延续
段是股价延续
 。现在老张决定取点
。现在老张决定取点
 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,
, ,
,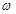 ,
, ,并且求得
,并且求得 。
。