题目内容
9、设一个等差数列，由三个数组成，三个数之和为9，三个数的平方和为35，则公差d=
±2
．分析：先设出这三个数，根据三个数之和为9，根据等差中项的性质求得a2，进而利用三个数的平方和，利用d表示出三个数建立等式求得d．
解答：解：设这三个数为a1，a2和a3，
a1+a2+a3=3a2=9，
∴a2=3
∵a12+a22+a32=（3-d）2+32+（3+d）2=9-6d+d2+9+9+6d+d2=27+2d2=35
∴d2=4
∴d=2或d=-2
故答案为：±2
a1+a2+a3=3a2=9，
∴a2=3
∵a12+a22+a32=（3-d）2+32+（3+d）2=9-6d+d2+9+9+6d+d2=27+2d2=35
∴d2=4
∴d=2或d=-2
故答案为：±2
点评：本题主要考查了等差数列的性质．灵活利用等差数列的等差中项的性质．注意等差数列项的设法a+d，a，a-d．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
=
．
= ．
=
。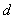