题目内容
设函数![]() 定义域为
定义域为![]() ,当
,当![]() 时,
时,![]() ,且对于任意的
,且对于任意的![]() ,都有
,都有![]()
(1)求![]() 的值,并证明函数
的值,并证明函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)记△ABC的三内角A、B、C的对应边分别为a,b,c,若![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
(1)![]() ,
,![]() ,故函数
,故函数![]() 在
在![]() 上是减函数。
上是减函数。
(2)![]()
解析:
(1) ![]() ,且当
,且当![]() 时,
时,![]() ,所以
,所以![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
, ![]()
对于![]() ,
,![]() ,设
,设![]() ,
,
则![]()
![]()
又![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
即 ![]() ,故函数
,故函数![]() 在
在![]() 上是减函数。
上是减函数。
(2)![]() 上单调递减,且
上单调递减,且![]()
所以![]()
![]()
![]()

练习册系列答案
相关题目
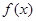 的定义域为
的定义域为 ,当
,当 时
时 的大小关系是( )
的大小关系是( ) B.
B.
 D.
D.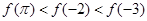
 的定义域为
的定义域为 .若当
.若当 时,
时,
 的解集是 .
的解集是 .
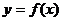 定义域为
定义域为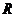 ,当
,当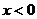 时,
时,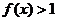 ,且对于任意的
,且对于任意的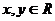 ,有
,有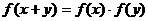 成立.数列
成立.数列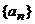 满足
满足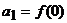 ,且
,且
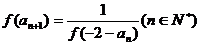 .
.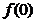 的值;
的值;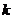 ,使
,使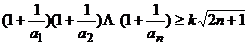 对一切
对一切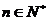 均成立,若存在,求出
均成立,若存在,求出