题目内容
已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,则球的半径等于分析:设出球的半径,小圆半径,通过已知条件求出两个半径,再求球的表面积.
解答: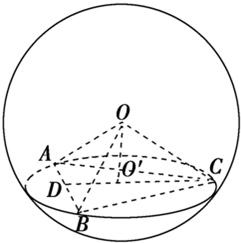 解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
则OO′⊥面ABC.在Rt△ACD中,cosA=
,则sinA=
.
在△ABC中,由正弦定理得
=2R,R=
,即O′C=
.
在Rt△OCO′中,由题意得r2-
r2=
,得r=
.
球的表面积S=4πr2=4π×
=54π.
故答案为:
、54π
 解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,则OO′⊥面ABC.在Rt△ACD中,cosA=
| 1 |
| 3 |
2
| ||
| 3 |
在△ABC中,由正弦定理得
| 6 |
| sinA |
| 9 |
| 4 |
| 2 |
| 9 |
| 4 |
| 2 |
在Rt△OCO′中,由题意得r2-
| 1 |
| 4 |
| 81×2 |
| 16 |
3
| ||
| 2 |
球的表面积S=4πr2=4π×
| 9×6 |
| 4 |
故答案为:
3
| ||
| 2 |
点评:本题考查球面距离弦长问题,正弦定理的应用,考查学生分析问题解决问题能力,空间想象能力,是中档题.

练习册系列答案
相关题目