题目内容
(本小题满分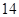 分)
分)
若函数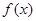 在定义域
在定义域 内某区间
内某区间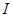 上是增函数,而
上是增函数,而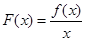 在
在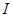 上是减函数,
上是减函数,
则称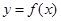 在
在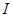 上是“弱增函数”
上是“弱增函数”
(1)请分别判断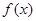 =
=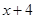 ,
,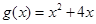 在
在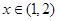 是否是“弱增函数”,
是否是“弱增函数”,
并简要说明理由;
(2)证明函数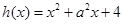 (
(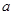 是常数且
是常数且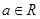 )在
)在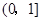 上是“弱增函数”.
上是“弱增函数”.
(1)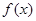 =
=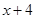 在
在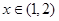 上是“弱增函数”;
上是“弱增函数”; 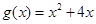 在
在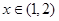 上不是“弱增函数”(2)易证
上不是“弱增函数”(2)易证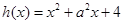 在
在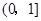 上是增函数,再利用定义证明
上是增函数,再利用定义证明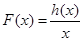 在
在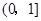 上是减函数
上是减函数
【解析】
试题分析:(1)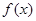 =
=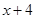 在
在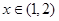 上是“弱增函数”;
上是“弱增函数”;
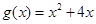 在
在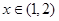 上不是“弱增函数”; ……2分
上不是“弱增函数”; ……2分
理由如下:
显然,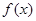 =
=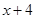 在
在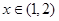 上是增函数,
上是增函数,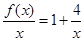 在
在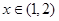 上是减函数,
上是减函数,
∴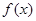 =
=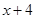 在
在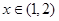 上是“弱增函数”。 ……4分
上是“弱增函数”。 ……4分
∵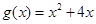 是开口向上的抛物线,对称轴方程为
是开口向上的抛物线,对称轴方程为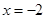 ,
,
∴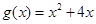 在
在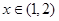 上是增函数,
上是增函数,
而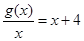 在
在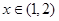 上是增函数,
上是增函数,
∴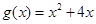 在
在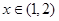 上不是“弱增函数”。 ……6分
上不是“弱增函数”。 ……6分
(2)证明:∵函数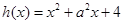 是开口向上的抛物线,对称轴方程为
是开口向上的抛物线,对称轴方程为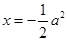 ,
,
∴函数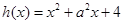 (
(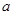 是常数且
是常数且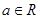 )在
)在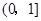 上是增函数; ……8分
上是增函数; ……8分
令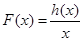 ,则
,则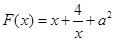 ,
,
对任意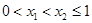 ,得
,得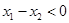 ,
,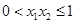 , ……9分
, ……9分
∵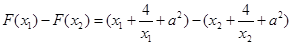
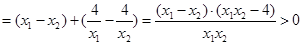 , ……12分
, ……12分
∴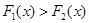 ,从而
,从而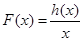 在
在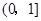 上是减函数, ……13分
上是减函数, ……13分
∴函数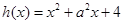 (
(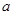 是常数且
是常数且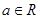 )在
)在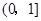 上是“弱增函数”. ……14分
上是“弱增函数”. ……14分
考点:本小题主要考查新定义下函数的单调性的研究和证明,考查学生的推理能力和论证能力.
点评:判断函数的单调性一是可以借助初等函数的单调性,再就是利用函数的单调性的定义来证明,利用定义证明函数的单调性时,要化到最简.

(本小题满分 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望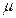 及标准差
及标准差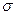 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在 范围中的学生的人数.
范围中的学生的人数.
(Ⅲ) 如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| | 身高达标 | 身高不达标 | 总计 |
| 积极参加体育锻炼 | 40 | | |
| 不积极参加体育锻炼 | | 15 | |
| 总计 | | | 100 |
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K
 =
=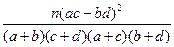 ,参考数据:
,参考数据:P(K  k) k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |

 分)已知
分)已知 ,
, ;
; ,求
,求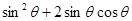 的值;
的值; ,
, ,求
,求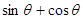 的值.
的值. 分)
分) ,
, ,
, ,且
,且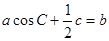 。
。 分)
分)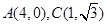 ,点M是OA的中点,点P在线段BC上运动(包括端点),如图
,点M是OA的中点,点P在线段BC上运动(包括端点),如图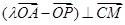 ?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。
?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。