题目内容
已知O为坐标原点,向量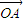 =(sinα,1),
=(sinα,1),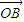 =(cosα,0),
=(cosα,0),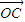 =(-sinα,2),点P是直线AB上的一点,且点B分有向线段
=(-sinα,2),点P是直线AB上的一点,且点B分有向线段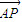 的比为1.
的比为1.(1)记函数f(α)=
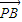 •
•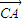 ,α∈(-
,α∈(-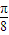 ,
,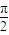 ),讨论函数f(α)的单调性,并求其值域;
),讨论函数f(α)的单调性,并求其值域;(2)若O,P,C三点共线,求|
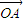 +
+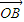 |的值.
|的值.
【答案】分析:(1)由已知中O为坐标原点,向量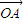 =(sinα,1),
=(sinα,1),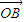 =(cosα,0),
=(cosα,0),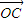 =(-sinα,2),点P是直线AB上的一点,且点B分有向线段
=(-sinα,2),点P是直线AB上的一点,且点B分有向线段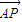 的比为1,我们代入定比分点坐标公式,可以求出点P的坐标,进而根据函数f(α)=
的比为1,我们代入定比分点坐标公式,可以求出点P的坐标,进而根据函数f(α)=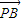 •
•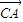 ,求出函数的解析式,利用除幂公式,及辅助解公式,将函数的解析式化为正弦型函数的形式后,结合α∈(-
,求出函数的解析式,利用除幂公式,及辅助解公式,将函数的解析式化为正弦型函数的形式后,结合α∈(-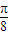 ,
,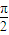 )及正弦函数的性质,我们即可求出函数f(α)的单调性,并求其值域;
)及正弦函数的性质,我们即可求出函数f(α)的单调性,并求其值域;
(2)若O,P,C三点共线,我们向量共线的充要条件,求出tanα的值,结合|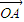 +
+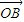 |=
|=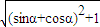 =
=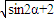 ,利用万能公式,代入即可求出|
,利用万能公式,代入即可求出|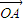 +
+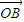 |的值.
|的值.
解答:解:依题意知:A(sinα,1),B(cosα,0),C(-sinα,2),
设点P的坐标为(x,y),
∵点B分有向线段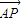 的比为1
的比为1
∴cosα=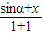 ,0=
,0=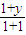 ,
,
∴x=2cosα-sinα,y=-1,
∴点P的坐标为(2cosα-sinα,-1)(2分)
(1)∵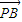 =(sinα-cosα,1),
=(sinα-cosα,1),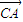 =(2sinα,-1)
=(2sinα,-1)
∴f(α)=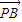 •
•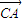 =2sin2α-2sinαcosα-1=-(sin2α+cos2α)=-
=2sin2α-2sinαcosα-1=-(sin2α+cos2α)=-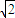 sin(2α+
sin(2α+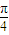 ),(4分)
),(4分)
由2α+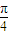 ∈(0,
∈(0,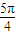 )可知函数f(α)的单调递增区间为(
)可知函数f(α)的单调递增区间为(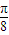 ,
,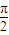 ),单调递减区间为(-
),单调递减区间为(-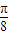 ,
,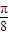 ),(6分)
),(6分)
所以sin(2α+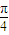 )∈(-
)∈(-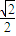 ,1],其值域为[-
,1],其值域为[-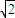 ,1);(8分)
,1);(8分)
(2)由O,P,C三点共线的-1×(-sinα)=2×(2cosα-sinα),
∴tanα= ,(10分)
,(10分)
∴sin2α=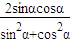 =
=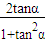 =
=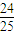 ,
,
∴|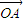 +
+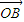 |=
|=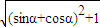 =
=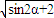 =
=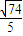 (12分)
(12分)
点评:本题考查的知识点是正弦型函数的单调性,两角和与差的正弦,二倍角的正弦,二倍角的余弦,三点共线,定比分点坐标公式,其中(1)的关键是根据已知条件求出函数f(α)=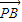 •
•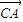 的解析式,并化简为正弦型函数的形式,将问题转化为确定正弦型函数的单调区间和值域,(2)的关键是根据向量共线的充要条件,求出tanα的值.
的解析式,并化简为正弦型函数的形式,将问题转化为确定正弦型函数的单调区间和值域,(2)的关键是根据向量共线的充要条件,求出tanα的值.
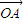 =(sinα,1),
=(sinα,1),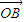 =(cosα,0),
=(cosα,0),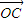 =(-sinα,2),点P是直线AB上的一点,且点B分有向线段
=(-sinα,2),点P是直线AB上的一点,且点B分有向线段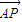 的比为1,我们代入定比分点坐标公式,可以求出点P的坐标,进而根据函数f(α)=
的比为1,我们代入定比分点坐标公式,可以求出点P的坐标,进而根据函数f(α)=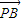 •
•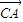 ,求出函数的解析式,利用除幂公式,及辅助解公式,将函数的解析式化为正弦型函数的形式后,结合α∈(-
,求出函数的解析式,利用除幂公式,及辅助解公式,将函数的解析式化为正弦型函数的形式后,结合α∈(-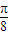 ,
,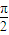 )及正弦函数的性质,我们即可求出函数f(α)的单调性,并求其值域;
)及正弦函数的性质,我们即可求出函数f(α)的单调性,并求其值域;(2)若O,P,C三点共线,我们向量共线的充要条件,求出tanα的值,结合|
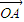 +
+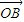 |=
|=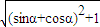 =
=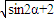 ,利用万能公式,代入即可求出|
,利用万能公式,代入即可求出|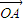 +
+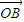 |的值.
|的值.解答:解:依题意知:A(sinα,1),B(cosα,0),C(-sinα,2),
设点P的坐标为(x,y),
∵点B分有向线段
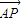 的比为1
的比为1∴cosα=
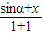 ,0=
,0=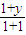 ,
,∴x=2cosα-sinα,y=-1,
∴点P的坐标为(2cosα-sinα,-1)(2分)
(1)∵
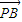 =(sinα-cosα,1),
=(sinα-cosα,1),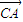 =(2sinα,-1)
=(2sinα,-1)∴f(α)=
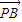 •
•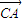 =2sin2α-2sinαcosα-1=-(sin2α+cos2α)=-
=2sin2α-2sinαcosα-1=-(sin2α+cos2α)=-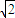 sin(2α+
sin(2α+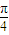 ),(4分)
),(4分)由2α+
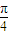 ∈(0,
∈(0,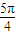 )可知函数f(α)的单调递增区间为(
)可知函数f(α)的单调递增区间为(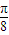 ,
,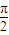 ),单调递减区间为(-
),单调递减区间为(-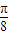 ,
,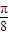 ),(6分)
),(6分)所以sin(2α+
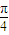 )∈(-
)∈(-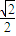 ,1],其值域为[-
,1],其值域为[-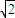 ,1);(8分)
,1);(8分)(2)由O,P,C三点共线的-1×(-sinα)=2×(2cosα-sinα),
∴tanα=
 ,(10分)
,(10分)∴sin2α=
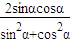 =
=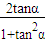 =
=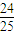 ,
,∴|
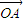 +
+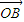 |=
|=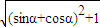 =
=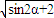 =
=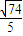 (12分)
(12分)点评:本题考查的知识点是正弦型函数的单调性,两角和与差的正弦,二倍角的正弦,二倍角的余弦,三点共线,定比分点坐标公式,其中(1)的关键是根据已知条件求出函数f(α)=
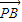 •
•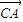 的解析式,并化简为正弦型函数的形式,将问题转化为确定正弦型函数的单调区间和值域,(2)的关键是根据向量共线的充要条件,求出tanα的值.
的解析式,并化简为正弦型函数的形式,将问题转化为确定正弦型函数的单调区间和值域,(2)的关键是根据向量共线的充要条件,求出tanα的值. 
练习册系列答案
相关题目
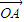 =(sinα,1),
=(sinα,1),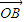 =(cosα,0),
=(cosα,0),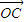 =(-sinα,2),点P是直线AB上的一点,且点B分有向线段
=(-sinα,2),点P是直线AB上的一点,且点B分有向线段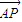 的比为1.
的比为1.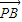 •
•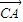 ,α∈(-
,α∈(-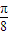 ,
,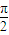 ),讨论函数f(α)的单调性,并求其值域;
),讨论函数f(α)的单调性,并求其值域;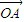 +
+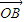 |的值.
|的值.