题目内容
3．将一个各个面上均涂有颜色的正方体锯成n3（n≥3）个同样大小的小正方体，从这些小正方体中任取1个，则其中三面都涂有颜色的概率为（ ）| A． | $\frac{1}{n^3}$ | B． | $\frac{4}{n^3}$ | C． | $\frac{8}{n^3}$ | D． | $\frac{1}{n^2}$ |
分析 试验发生包含的事件是正方体锯成n3个同样大小的小正方体，共有n3个结果，然后计算出满足条件三面都涂有颜色的基本事件个数，代入古典概型概率公式即可得到答案．
解答 解：由题意知本题是一个古典概型，
试验发生包含的事件是正方体锯成n3个同样大小的小正方体，共有n3个结果，
满足条件的事件是三面都涂有颜色，出现各个顶点上，共有8个，
根据古典概型概率公式得到$\frac{8}{{n}^{3}}$，
故选：C．
点评 古典概型要求能够列举出所有事件和发生事件的个数，概率问题同其他的知识点结合在一起，实际上是以概率问题为载体，主要考查的是另一个知识点，本题主要考查正方体的结构．
练习册系列答案
相关题目
11．函数y=loga（2x-3）+$\frac{\sqrt{2}}{2}$（a＞0且a≠1）的图象恒过定点P，且P在幂函数f（x）的图象上，则f（4）=（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | 16 |
18．已知动圆M过定点B（-4，0），且和定圆（x-4）2+y2=16相外切，则动圆圆心M的轨迹方程为（ ）
| A． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1（x＞0） | B． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1（x＜0） | C． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | D． | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1 |
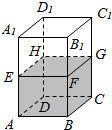如图所示，在透明塑料制成的长方体容器ABCD-A1B1C1D1灌进一些水，将容器底面的一边BC固定于地面上，再将容器倾斜，随着倾斜程度的不同，有以下命题：
15．设a=log50.5，b=log20.3，c=log0.32则（ ）
| A． | b＜a＜c | B． | b＜c＜a | C． | c＜b＜a | D． | a＞b＞c |
