题目内容

（2010•石家庄二模）已知四棱锥S-ABCD，底面是边长为1的正方形，SD⊥底面ABCD，SD=
3
，E为AB上的一个动点，则SE+CE的最小值为（　　）
分析：设AE=x，则BE=1-x，SE+CE表示平面内的动点到A（0，2）与B（1，1）的距离和，取B（1，1）关于x轴的对称点B′（1，-1），则可求SE+CE的最小值．
解答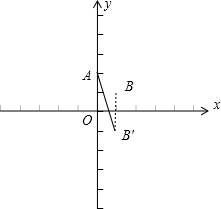：解：设AE=x，则BE=1-x
∴SE=
x2+4
，CE=
(x-1)2+1

∴SE+CE=
x2+4
+
(x-1)2+1

如右图所示，则SE+CE表示在x轴上的点到A（0，2）与B（1，1）的距离和
取B（1，1）关于x轴的对称点B′（1，-1）
则SE+CE的最小值为AB′=
(0-1)2+(2+1)2
=
10

故选B．
点评：本题以四棱锥S-ABCD为载体，考查线段和的最小值，解题的关键是表示出距离的和，利用对称性求解．
练习册系列答案
相关题目
（2010•石家庄二模）已知定义域为R的函数f（x）在（1，+∞）上为减函数，且函数y=f（x+1）为偶函数，则（　　）
（2010•石家庄二模）若函数y=f（x）的图象如图①所示，则图②对应函数的解析式可以表示为（　　）
（2010•石家庄二模）已知△ABC中，内角A、B、C的对边的边长为a、b、c，且bcosC=（2a-c）cosB．
（Ⅰ）求角B的大小；
（Ⅱ）若y=cos2A+cos2C，求y的最小值．
（2010•石家庄二模）已知动圆M经过点G（0，-1），且与圆Q：x2+（y-1）2=8内切．
（Ⅰ）求动圆M的圆心的轨迹E的方程．
（Ⅱ）以m=(1，
2
)为方向向量的直线l交曲线E于不同的两点A、B，在曲线E上是否存在点P使四边形OAPB为平行四边形（O为坐标原点）．若存在，求出所有的P点的坐标与直线l的方程；若不存在，请说明理由．
（2010•石家庄二模）如图，已知全集为U，A，B是U的两个子集，则阴影部分所表示的集合是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网