题目内容
若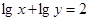 ,则
,则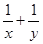 的最小值为_____________
的最小值为_____________
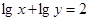 ,则
,则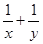 的最小值为_____________
的最小值为_____________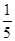
考点:
分析:根据对数的运算性质计算已知的等式,得到xy的值,且由对数函数的定义域得到x与y都大于0,然后把所求的式子通分后,利用分子利用基本不等式变形,将xy的值代入即可求出所求式子的最小值.
解答:解:由lgx+lgy=lgxy=2,得到xy=10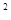 =100,且x>0,y>0,
=100,且x>0,y>0,
∴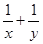 =
=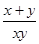 ≥
≥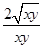 =
=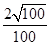 =
=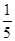
,当且仅当x=y时取等号,
则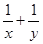 的最小值为
的最小值为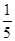 .
.
故答案为: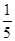
分析:根据对数的运算性质计算已知的等式,得到xy的值,且由对数函数的定义域得到x与y都大于0,然后把所求的式子通分后,利用分子利用基本不等式变形,将xy的值代入即可求出所求式子的最小值.
解答:解:由lgx+lgy=lgxy=2,得到xy=10
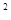 =100,且x>0,y>0,
=100,且x>0,y>0,∴
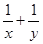 =
=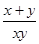 ≥
≥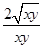 =
=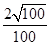 =
=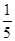
,当且仅当x=y时取等号,
则
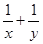 的最小值为
的最小值为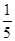 .
.故答案为:
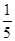

练习册系列答案
相关题目
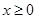 ,则
,则  的最小值是
的最小值是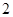
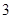
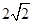
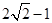
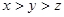 ,
,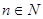 ,且
,且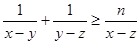 恒成立,则
恒成立,则 的最大值为( )
的最大值为( )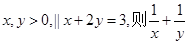 的最小值为 ( )
的最小值为 ( )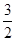
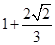
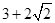
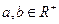 ,且
,且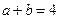 ,则
,则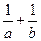 的最小值为_________________.
的最小值为_________________. 满足
满足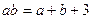 ,则
,则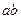 的取值范围是_______
的取值范围是_______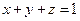 ,则
,则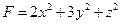 的最小值为_____________。
的最小值为_____________。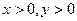 ,且
,且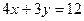 ,则
,则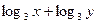 的最大值是 ( )
的最大值是 ( )