题目内容
已知直线a,b,c和平面α,β,下列命题中正确的是
①若a∥α,b?α,则a∥b
②若a∥α,b∥α,则a∥b
③若a∥b,b?α,则a∥α④若a∥b,a∥α,则b?α或b∥α
⑤若a∥α,a∥β,α∩β=c,则a∥c⑥若α⊥β,α∩β=b,a⊥b,则a⊥β
④⑤
④⑤
(填序号)①若a∥α,b?α,则a∥b
②若a∥α,b∥α,则a∥b
③若a∥b,b?α,则a∥α④若a∥b,a∥α,则b?α或b∥α
⑤若a∥α,a∥β,α∩β=c,则a∥c⑥若α⊥β,α∩β=b,a⊥b,则a⊥β
分析:根据线面平行的性质定理的条件判断①是否正确;
利用图形演示判断②是否正确;
根据线面平行的判定定理的条件判断③是否正确;
结合图形,判断线面的可能情况.判定④的正确性;
利用图形,结合线面平行的性质判断⑤是否正确;
利用图形,判断线面的可能情况,判断⑥是否正确.
利用图形演示判断②是否正确;
根据线面平行的判定定理的条件判断③是否正确;
结合图形,判断线面的可能情况.判定④的正确性;
利用图形,结合线面平行的性质判断⑤是否正确;
利用图形,判断线面的可能情况,判断⑥是否正确.
解答:解:①a∥α,b?α,a、b的位置关系是平行或异面,∴①错误;
②a∥α,b∥α,a、b的位置关系是平行、相交或异面,∴②错误;
③a∥b,b?α,a可能在α内.∴③错误;
④a∥b,a∥α过a作平面β,α∩β=c,b∥c,∴b∥α或b?α,∴④正确;
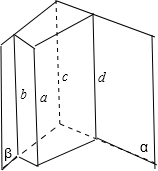
⑤a∥α,a∥β,α∩β=c,如图,过a作两相交平面分别交α、β于b、d,由线面平行的性质得a∥b∥d,∴b∥α,∴b∥c,∵a∥b,∴a∥c,故⑤正确;
⑥∵α⊥β,α∩β=b,a⊥b,a与β有可能平行、相交.∴⑥错误.
故答案是④⑤
②a∥α,b∥α,a、b的位置关系是平行、相交或异面,∴②错误;
③a∥b,b?α,a可能在α内.∴③错误;
④a∥b,a∥α过a作平面β,α∩β=c,b∥c,∴b∥α或b?α,∴④正确;
⑤a∥α,a∥β,α∩β=c,如图,过a作两相交平面分别交α、β于b、d,由线面平行的性质得a∥b∥d,∴b∥α,∴b∥c,∵a∥b,∴a∥c,故⑤正确;

⑥∵α⊥β,α∩β=b,a⊥b,a与β有可能平行、相交.∴⑥错误.
故答案是④⑤
点评:本题借助考查命题的真假判断,考查空间线面、线线关系的判定.

练习册系列答案
相关题目