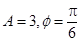题目内容
 已知函数
已知函数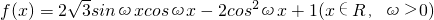 的周期为π.
的周期为π.
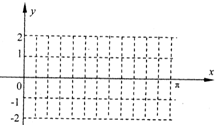
(Ⅰ)利用五点作图法作出y=f(x)在x∈[0,π]一个周期上的图象;
(Ⅱ)当 时,若f(θ)=1,求θ值.
时,若f(θ)=1,求θ值.
解:(1)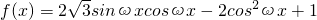
= sin2ωx-cosωx
sin2ωx-cosωx
=2sin(2ωx- ).
).
∵T=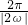 =π,ω>0,
=π,ω>0,
∴ω=1.
∴f(x)2sin(2x- ).
).
列表
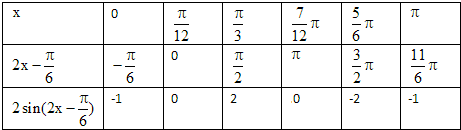
函数的图象为:
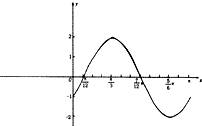
(2)∵2sin(2 )=1,
)=1,
∴2sin(2 )=
)= ,
,
∵ ,
,
∴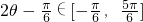
∴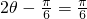 ,或
,或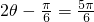
∴ 或
或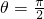 .
.
分析:(1)通过二倍角公式以及两角差的正弦函数化简函数为 一个角的一个三角函数的形式,直接利用函数的周期,求解函数的解析式,然后列表,画出函数的图象.
(2)利用函数的解析式通过f(θ)=1,以及θ的范围,直接求出θ的值.
点评:本题考查五点法作函数y=Asin(ωx+φ)的图象,三角函数的化简求值,正弦函数的定义域和值域,考查作图能力,计算能力.
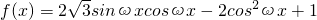
=
 sin2ωx-cosωx
sin2ωx-cosωx=2sin(2ωx-
 ).
).∵T=
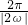 =π,ω>0,
=π,ω>0,∴ω=1.
∴f(x)2sin(2x-
 ).
).列表

函数的图象为:

(2)∵2sin(2
 )=1,
)=1,∴2sin(2
 )=
)= ,
,∵
 ,
,∴
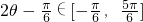
∴
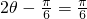 ,或
,或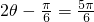
∴
 或
或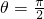 .
.分析:(1)通过二倍角公式以及两角差的正弦函数化简函数为 一个角的一个三角函数的形式,直接利用函数的周期,求解函数的解析式,然后列表,画出函数的图象.
(2)利用函数的解析式通过f(θ)=1,以及θ的范围,直接求出θ的值.
点评:本题考查五点法作函数y=Asin(ωx+φ)的图象,三角函数的化简求值,正弦函数的定义域和值域,考查作图能力,计算能力.

练习册系列答案
相关题目
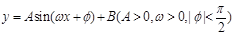 的周期为T,在一个周期内的图像如图所示,则正确的结论是( )
的周期为T,在一个周期内的图像如图所示,则正确的结论是( )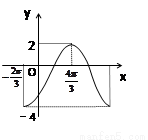
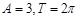 B.
B.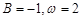
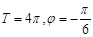 D.
D.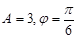
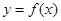 的周期为2,当
的周期为2,当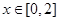 时,
时,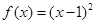 ,如果
,如果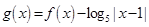 则函数
则函数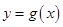 的所有零点之和为:
的所有零点之和为: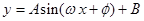 (
(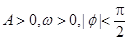 )的周期为
)的周期为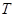 ,在一个周期内的图象如图所示,则正确的结论是( ).
,在一个周期内的图象如图所示,则正确的结论是( ).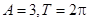 B.
B.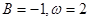
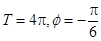 D.
D.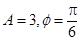
 (
(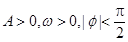 )
)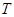 ,在一个周期内的图象如图所示,
,在一个周期内的图象如图所示,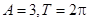 B.
B.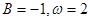
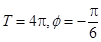 D.
D.