题目内容
若集合M = {x ∈R | 2 x ≥ 4},N = {x∈R | x 2 - 4 x + 3 ≥ 0},则M∩N =
- A.{x | x≤ 4}
- B.{x | x≤ 1}
- C.{x | x≥ 2}
- D.{x | x≥ 3}
D
试题分析:根据题意,由于指数函数的单调性可知集合M = {x ∈R | 2 x ≥ 4}={x|x≥2},而根据一元二次不等式的求解可知N = {x∈R | x 2 - 4 x + 3 ≥ 0}=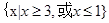 ,那么可知M∩N=
,那么可知M∩N=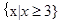 ,故选D.
,故选D.
考点:集合的交集
点评:解决的关键是对于指数函数的单调性和一元二次不等式的求解,属于基础题。
试题分析:根据题意,由于指数函数的单调性可知集合M = {x ∈R | 2 x ≥ 4}={x|x≥2},而根据一元二次不等式的求解可知N = {x∈R | x 2 - 4 x + 3 ≥ 0}=
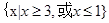 ,那么可知M∩N=
,那么可知M∩N=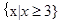 ,故选D.
,故选D.考点:集合的交集
点评:解决的关键是对于指数函数的单调性和一元二次不等式的求解,属于基础题。

练习册系列答案
相关题目