题目内容
若a1>0,a1≠1,an+1=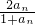 (n=1,2,…)
(n=1,2,…)
(1)求证:an+1≠an;
(2)令a1= ,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an.
,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an.
解:(1)证明:若an+1=an,
即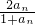 =an,解得an=0或1.
=an,解得an=0或1.
从而an=an-1=…a2=a1=0或1,与题设a1>0,a1≠1相矛盾,
故an+1≠an成立.
(2)由a1= ,得到a2=
,得到a2= =
= =
= ,
,
a3= =
= =
= ,
,
a4= =
= =
= ,
,
a5= =
=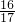 =
=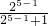 ,
,
…,
则an= (n∈N*).
(n∈N*).
分析:(1)采用反证法证明,先假设两种相等,代入已知的等式中即可求出an的值为常数0或1,进而得到此数列为是0或1的常数列,与已知a1>0,a1≠1矛盾,所以假设错误,两种不相等;
(2)把n=1及a1= 代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值,把n=4及a4的值代入已知的等式即可求出a5的值,然后把求出的五项的值变形后,即可归纳总结得到这个数列的通项公式an.
代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值,把n=4及a4的值代入已知的等式即可求出a5的值,然后把求出的五项的值变形后,即可归纳总结得到这个数列的通项公式an.
点评:此题考查学生会利用反证法对命题进行证明的能力,会根据一组数据的特点归纳总结得出一般性的规律,是一道中档题.
即
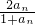 =an,解得an=0或1.
=an,解得an=0或1.从而an=an-1=…a2=a1=0或1,与题设a1>0,a1≠1相矛盾,
故an+1≠an成立.
(2)由a1=
 ,得到a2=
,得到a2= =
= =
= ,
,a3=
 =
= =
= ,
,a4=
 =
= =
= ,
,a5=
 =
=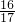 =
=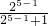 ,
,…,
则an=
 (n∈N*).
(n∈N*).分析:(1)采用反证法证明,先假设两种相等,代入已知的等式中即可求出an的值为常数0或1,进而得到此数列为是0或1的常数列,与已知a1>0,a1≠1矛盾,所以假设错误,两种不相等;
(2)把n=1及a1=
 代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值,把n=4及a4的值代入已知的等式即可求出a5的值,然后把求出的五项的值变形后,即可归纳总结得到这个数列的通项公式an.
代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值,把n=4及a4的值代入已知的等式即可求出a5的值,然后把求出的五项的值变形后,即可归纳总结得到这个数列的通项公式an.点评:此题考查学生会利用反证法对命题进行证明的能力,会根据一组数据的特点归纳总结得出一般性的规律,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (n=1,2,…)
(n=1,2,…) ,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an;
,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an; 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值. (n=1,2,…)
(n=1,2,…) ,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an.
,写出a2、a3、a4、a5的值,观察并归纳出这个数列的通项公式an.