题目内容
已知函数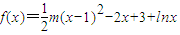 ,常数m≥1
,常数m≥1(1)求函数f(x)单调递减区间;
(2)当m=2时,设函数g(x)=f(x)-f(2-x)+3的定义域为D,?x1,x2∈D,且x1+x2=1,求证:g(x1)+g(x2),g(x1)-g(x2),g(2x1)+g(2x2),g(2x1)-g(2x2)中必有一个是常数(不含x1,x2);
(3)若曲线C:y=f(x)在点P(1,1)处的切线l与曲线C有且只有一个公共点,求m的值.
【答案】分析:(1)先利用导数四则运算计算函数f(x)的导函数f′(x),再解不等式f′(x)<0,即可得函数的单调减区间
(2)先证明函数g(x)关于(1,3)中心对称,再结合x1+x2=1,即可证明g(2x1)+g(2x2)=6为常数,也可代入函数解析式直接证明结论
(3)先利用导数的几何意义,求切线l的方程,再与曲线联立,得关于x的方程,再将方程有且只有一解转化为函数有且只有一个零点问题,利用导数,通过讨论所研究函数的单调性和极值,可得m的值
解答:解:(1)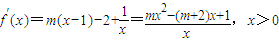
对于y=mx2-(m+2)x+1而言,
∵m≥1,∴△=(m+2)2-4m=m2+4>0
且它的两个零点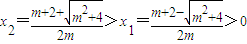
故当x1<x<x2时f′(x)<0
∴函数f(x)的单调减区间为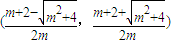
(2)法一:g(x)=4-4x+lnx-ln(2-x)+3关于点A(1,3)对称,证明如下:
设P(x,y)为y=g(x)图象上任意一点,P关于点A(1,3)的对称点为P′(2-x,6-y).
∵y=4-4x+lnx-ln(2-x)+3,∴6-y=4-4(2-x)+ln(2-x)-ln(2-(2-x))+3
∴P′也在函数y=g(x)图象上,故y=g(x)图象关于点A(1,3)对称
∵2x1+2x2=2,∴g(2x1)+g(2x2)=6为常数
法二: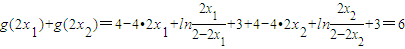 为常数
为常数
(3)∵f′(1)=-1,∴直线l:y-1=-(x-1),即y=2-x
代入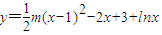
得m(x-1)2-2x+2lnx+2=0
令F(x)=m(x-1)2-2x+2lnx+2,则F(1)=0,∴F(x)=0有一个解x=1
又∵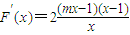
①当m=1时,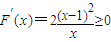 ,∴F(x)在(0,+∞)上递增,∴F(x)=0恰有一个解符合条件;
,∴F(x)在(0,+∞)上递增,∴F(x)=0恰有一个解符合条件;
②当m>1时,当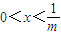 或x>1时,F′(x)>0,当
或x>1时,F′(x)>0,当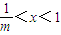 时F′(x)<0,
时F′(x)<0,
故F(x)极大值=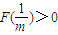 ,极小值F(1)=0.
,极小值F(1)=0.
且当x→0时F(x)→-∞;当x→+∞时,F(x)→+∞
∴F(x)在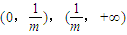 上各有一个实根,不符合条件,舍去
上各有一个实根,不符合条件,舍去
综上m=1
点评:本题综合考查了利用导数求函数的单调区间,利用导数的几何意义求切线方程,利用导数研究函数的极值,进而解决零点分布问题.
(2)先证明函数g(x)关于(1,3)中心对称,再结合x1+x2=1,即可证明g(2x1)+g(2x2)=6为常数,也可代入函数解析式直接证明结论
(3)先利用导数的几何意义,求切线l的方程,再与曲线联立,得关于x的方程,再将方程有且只有一解转化为函数有且只有一个零点问题,利用导数,通过讨论所研究函数的单调性和极值,可得m的值
解答:解:(1)
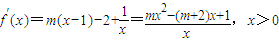
对于y=mx2-(m+2)x+1而言,
∵m≥1,∴△=(m+2)2-4m=m2+4>0
且它的两个零点
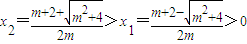
故当x1<x<x2时f′(x)<0
∴函数f(x)的单调减区间为
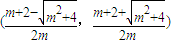
(2)法一:g(x)=4-4x+lnx-ln(2-x)+3关于点A(1,3)对称,证明如下:
设P(x,y)为y=g(x)图象上任意一点,P关于点A(1,3)的对称点为P′(2-x,6-y).
∵y=4-4x+lnx-ln(2-x)+3,∴6-y=4-4(2-x)+ln(2-x)-ln(2-(2-x))+3
∴P′也在函数y=g(x)图象上,故y=g(x)图象关于点A(1,3)对称
∵2x1+2x2=2,∴g(2x1)+g(2x2)=6为常数
法二:
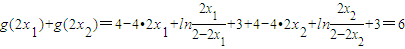 为常数
为常数(3)∵f′(1)=-1,∴直线l:y-1=-(x-1),即y=2-x
代入
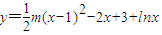
得m(x-1)2-2x+2lnx+2=0
令F(x)=m(x-1)2-2x+2lnx+2,则F(1)=0,∴F(x)=0有一个解x=1
又∵
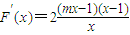
①当m=1时,
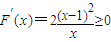 ,∴F(x)在(0,+∞)上递增,∴F(x)=0恰有一个解符合条件;
,∴F(x)在(0,+∞)上递增,∴F(x)=0恰有一个解符合条件;②当m>1时,当
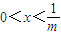 或x>1时,F′(x)>0,当
或x>1时,F′(x)>0,当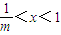 时F′(x)<0,
时F′(x)<0,故F(x)极大值=
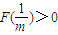 ,极小值F(1)=0.
,极小值F(1)=0.且当x→0时F(x)→-∞;当x→+∞时,F(x)→+∞
∴F(x)在
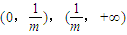 上各有一个实根,不符合条件,舍去
上各有一个实根,不符合条件,舍去综上m=1
点评:本题综合考查了利用导数求函数的单调区间,利用导数的几何意义求切线方程,利用导数研究函数的极值,进而解决零点分布问题.

练习册系列答案
相关题目
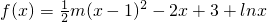 ,常数m≥1
,常数m≥1 其中常数
其中常数 .
. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 时,若函数
时,若函数 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围; 在点
在点 处的切线方程为
处的切线方程为 当
当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.