Question

已知圆x²+y²=1，点A（1，0），△ABC内接于圆，且∠BAC=60°，当B、C在圆上运动时，BC中点的轨迹方程是（　　）

• A、x²+y²=

  1

  2

• B、x²+y²=

  1

  4

• C、x²+y²=

  1

  2

  （x＜

  1

  2

  ）
• D、x²+y²=

  1

  4

  （x＜

  1

  4

  ）

Answer 1

分析：将圆周角为定值转化为圆心角为定值，结合圆心距构成的直角三角形得OD=

1

2

，从而得BC中点的轨迹方程．

解答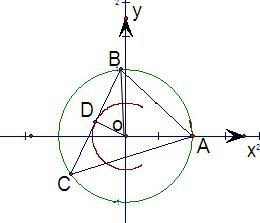：解：设BC中点是D，
∵圆心角等于圆周角的一半，
∴∠BOD=60°，
在直角三角形BOD中，有OD=

1

2

OB=

1

2

，
故中点D的轨迹方程是：x²+y²=

1

4

，
如图，由角BAC的极限位置可得，x＜

1

4

，
故选D．

点评：本题主要考查求轨迹方程，解决与平面几何有关的轨迹问题时，要充分考虑到图形的几何性质，这样会使问题的解决简便些．