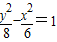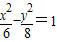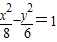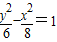题目内容
经过点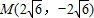 且与双曲线
且与双曲线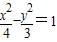 有共同渐近线的双曲线方程为( )
有共同渐近线的双曲线方程为( )A.
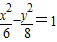
B.
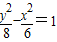
C.
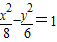
D.
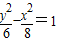
【答案】分析:根据有相同的渐近线可设所求双曲线为 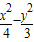 =λ (λ≠0),把点
=λ (λ≠0),把点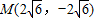 代入,解得:λ的值,进而求出答案.
代入,解得:λ的值,进而求出答案.
解答:解:由题意可得:设所求双曲线为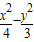 =λ (λ≠0),
=λ (λ≠0),
把点M(2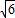 ,-2
,-2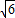 ),解得
),解得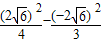 =λ=-2,
=λ=-2,
∴所求的双曲线方程为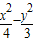 =-2,即
=-2,即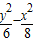 =1.
=1.
故选:D.
点评:本题考查双曲线的性质和应用,解题时要注意待定系数法的合理运用.
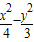 =λ (λ≠0),把点
=λ (λ≠0),把点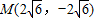 代入,解得:λ的值,进而求出答案.
代入,解得:λ的值,进而求出答案.解答:解:由题意可得:设所求双曲线为
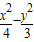 =λ (λ≠0),
=λ (λ≠0),把点M(2
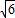 ,-2
,-2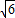 ),解得
),解得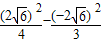 =λ=-2,
=λ=-2,∴所求的双曲线方程为
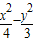 =-2,即
=-2,即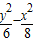 =1.
=1.故选:D.
点评:本题考查双曲线的性质和应用,解题时要注意待定系数法的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
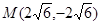 且与双曲线
且与双曲线 有共同渐近线的双曲线方程为( )
有共同渐近线的双曲线方程为( )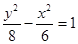 B、
B、
 D、
D、
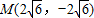 且与双曲线
且与双曲线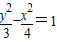 有共同渐近线的双曲线方程为( )
有共同渐近线的双曲线方程为( )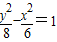
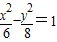
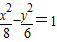
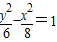
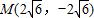 且与双曲线
且与双曲线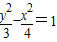 有共同渐近线的双曲线方程为( )
有共同渐近线的双曲线方程为( )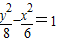
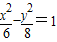
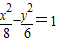
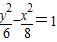
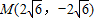 且与双曲线
且与双曲线 有共同渐近线的双曲线方程为( )
有共同渐近线的双曲线方程为( )