题目内容
计算下列几个式子:
①2(sin35°cos25°+sin55°cos65°),
② ,
,
③ ,
,
④ ,
,
⑤
结果为 的是 (填上所有你认为正确答案的序号)
的是 (填上所有你认为正确答案的序号)
①②④⑤
解析试题分析:2(sin35°cos25°+sin55°cos65°)=2(sin35°cos25°+cos35°sin25°)=2sin60°= ,①符合;∵tan60°=tan(25°+35°)=
,①符合;∵tan60°=tan(25°+35°)=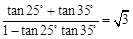 ,∴tan25°+tan35°=
,∴tan25°+tan35°= (1-tan25°tan35°),∴t
(1-tan25°tan35°),∴t =
= ,②符合;
,②符合;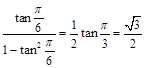 ,③不符合;
,③不符合; ═tan(45°+15°)=tan60°=
═tan(45°+15°)=tan60°= ,④符合;
,④符合;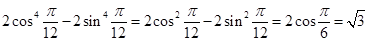 ,⑤符合,综上,符合题意的序号为①②④⑤
,⑤符合,综上,符合题意的序号为①②④⑤
考点:本题考查了三角函数的变换及求值
点评:对于此类三角函数的化简求值问题,考查了学生对三角函数基础公式的理解和灵活一运用,属基础题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,且
,且 ,则角
,则角 的取值范围是 .
的取值范围是 . ,
, ,则
,则 的值是_________;
的值是_________; = .
= .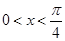 ,
,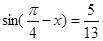 ,则
,则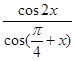 值为________________.
值为________________. ________
________ 且
且 ,则
,则 .
. ,则
,则
 ,且
,且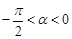 ,则
,则 .
.