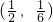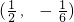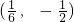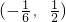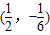Question

若m，n满足m+2n-1=0，则直线mx+3y+n=0过定点（　　）

• A．(

  1

  2

  ，

  1

  6

  )
• B．(

  1

  2

  ，-

  1

  6

  )
• C．(

  1

  6

  ，-

  1

  2

  )
• D．(-

  1

  6

  ，

  1

  2

  )

Answer 1

分析：将题中条件：“m+2n-1=0”代入直线方程，得直线即n（1-2x）+（x+3y）=0，一定经过1-2x=0和x+3y=0的交点．

解答：解：∵m+2n-1=0，
∴m=1-2n，代入直线mx+3y+n=0方程得，
n（1-2x）+（x+3y）=0，
它经过1-2x=0 和x+3y=0 的交点(

1

2

，-

1

6

)，
故选B．

点评：本题考查直线过定点问题，两直线的交点坐标的求法，利用m（x+2）+（y-1）=0，经过x+2=0和y-1=0 的交点．