题目内容
已知m,n为两个不相等的非零实数,则方程mx-y+n=0与nx2+my2=mn所表示的曲线可能是( )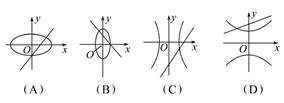
C
解析
练习册系列答案
相关题目
过抛物线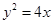
焦点
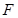的直线交其于
，
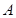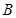两点，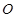
为坐标原点．若
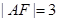，则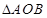
的面积为（ ）
A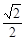． | B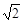． | C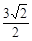． | D．2 |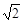
(B)
(C)
(D)
已知抛物线x2=4y上有一条长为6的动弦AB,则AB中点到x轴的最短距离为( )
A． | B． | C．1 | D．2 |
若已知点Q(4,0)和抛物线y=
x2+2上一动点P(x,y),则y+|PQ|最小值为( )
A．2+2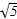 | B．11 | C．1+2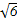 | D．6 |
已知点F(
,0),直线l:x=-,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹是( )
| A．双曲线 | B．椭圆 |
| C．圆 | D．抛物线 |
若抛物线y2=2px(p>0)的焦点在圆x2+y2+2x-3=0上,则p=( )
A． | B．1 | C．2 | D．3 |
已知M是y=
x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为( )
| A．2 | B．4 | C．8 | D．10 |
以抛物线y2＝8x上的任意一点为圆心作圆与直线x＋2＝0相切，这些圆必过一定点，则这一定点的坐标是( )
| A．(0，2) | B．(2，0) |
| C．(4，0) | D．(0，4) |