题目内容
已知定义在R上的连续函数y=f(x)对任意x满足f(3-x)=f(x),(x-
)f′(x)>0,则下列命题正确的有
①函数y=f(x+
)为偶函数;
②若x1<x2且x1+x2>3,则f(x1)<f(x2);
③f(
)>f(sin14°+cos14°);
④若f(
)•f(5)<0,则y=f(x)有两个零点.
| 3 |
| 2 |
①②④
①②④
.①函数y=f(x+
| 3 |
| 2 |
②若x1<x2且x1+x2>3,则f(x1)<f(x2);
③f(
| 2 |
④若f(
| 3 |
| 2 |
分析:根据函数的对称性,求出函数y=f(x)的对称轴,进而根据函数图象的平移变换,求出函数y=f(x+
)的对称轴,可判断①;根据已知结合导数符号与原函数单调性的关系,分析出函数的单调性,进而可判断②,③,再结合零点存在定理可判断④
| 3 |
| 2 |
解答:解:①∵函数y=f(x)对任意x满足f(3-x)=f(x),
故函数y=f(x)的图象关于直线x=
对称
函数y=f(x+
)的图象由函数y=f(x)的图象向左平移
个单位得到,故关于y轴对称,函数y=f(x+
)为偶函数,即①正确;
②∵(x-
)f′(x)>0,故x>
时,f′(x)>0,f(x)为增函数,
x<
时,f′(x)<0,f(x)为减函数,
若x1<x2且x1+x2>3,则f(x1)<f(x2),故②正确;
③sin14°+cos14°=
sin(14°+45°)=
sin59°,∵
>
sin59°,且
+
sin59°<3,故f(
)<f(sin14°+cos14°),即③错误;
④若f(
)•f(5)<0,则函数若f(
)<0,f(-2)=f(5)>0,由函数的单调性及零点存在定理,可得y=f(x)有两个零点,故④正确
故正确的命题有:①②④
故答案为:①②④
故函数y=f(x)的图象关于直线x=
| 3 |
| 2 |
函数y=f(x+
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
②∵(x-
| 3 |
| 2 |
| 3 |
| 2 |
x<
| 3 |
| 2 |
若x1<x2且x1+x2>3,则f(x1)<f(x2),故②正确;
③sin14°+cos14°=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
④若f(
| 3 |
| 2 |
| 3 |
| 2 |
故正确的命题有:①②④
故答案为:①②④
点评:本题以命题的真假判断为载体考查了函数的对称性,奇偶性,单调性,零点等知识点,综合性强,难度较大.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
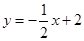 ,则
,则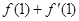 等于(
)
等于(
)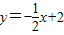 ,则f(1)+f′(1)= .
,则f(1)+f′(1)= .