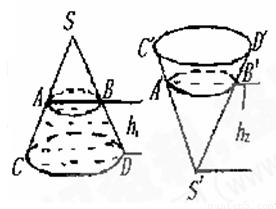
题目内容
 如图,圆锥形封闭容器,高为h,圆锥内水面高为h1,h1=
如图,圆锥形封闭容器,高为h,圆锥内水面高为h1,h1=| h | 4 |
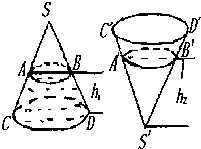
分析:圆锥正置与倒置时,水的体积不变,而水面是平行于底面的平面,此平面截得的小圆锥与原圆锥成相似体,它们的体积之比为对应高的立方比,由此结合题中数据加以计算,即可得到h2的大小.
解答: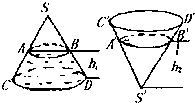 解:∵圆锥内水面高为h1满足h1=
解:∵圆锥内水面高为h1满足h1=
,
∴两个圆锥体积之比为
=(
)3=
即水的体积与容器体积之比为1-
=
,
由此可得:倒置后
=
=
∴(
)3=
,得
=
,即h2=
h.
 解:∵圆锥内水面高为h1满足h1=
解:∵圆锥内水面高为h1满足h1=| h |
| 4 |
∴两个圆锥体积之比为
| VS-AB |
| VS-CD |
| 3 |
| 4 |
| 27 |
| 64 |
即水的体积与容器体积之比为1-
| 27 |
| 64 |
| 37 |
| 64 |
由此可得:倒置后
| V水 |
| VS-C‘D’ |
| h23 |
| h3 |
| 37 |
| 64 |
∴(
| h2 |
| h |
| 37 |
| 64 |
| h2 |
| h |
| |||
| 4 |
| |||
| 4 |
点评:本题给出密闭圆锥容器,给出里面的一定量的水,已知正放的情况下水面的高度,求倒置后水面的高度.着重考查了圆锥的体积公式、圆锥的平行截面的性质及其应用等知识,属于中档题.

练习册系列答案
相关题目
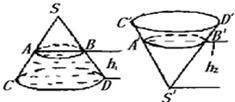 如图,圆锥形封闭容器,高为h,圆锥内水面高为
如图,圆锥形封闭容器,高为h,圆锥内水面高为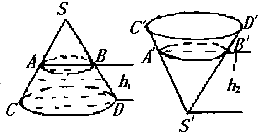 如图,圆锥形封闭容器,高为h,圆锥内水面高为
如图,圆锥形封闭容器,高为h,圆锥内水面高为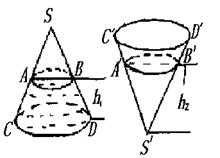
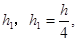 若将圆锥倒置后,圆锥内水面高为
若将圆锥倒置后,圆锥内水面高为