题目内容

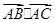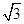已知M 是△ABC内的一点（不含边界），且=" 2" , ∠BAC =30°，若△MBC，△MCA和△MAB的面积分别为x，y，z，记f(x,y，z)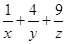＝，则f（x,y,z）的最小值是＿＿

 

【答案】

36

【解析】

试题分析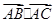：=" 2" 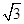=AB?AC?cos30°，∴AB?AC=4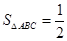，AB?AC?sin30°=1=x+y+z，∴f（x，y，z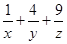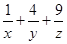）==（）（x+y+z）

=1+4+9+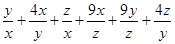≥14+4+6+12=36

考点：本题考查了向量的应用，以及三角形的面积公式，同时考查了均值不等式的应用

点评：求解向量与三角的综合应用问题，要能够将向量实数化，常常涉及数量积运算，具体问题中要再很大成大程度上发挥向量的“数”的特征.本题显然涉及考查均值不等式，要能够构造均值不等式应用的条件“积为定值”，同时注意取等条件的验证

 

练习册系列答案
相关题目
已知M是△ABC内的一点（不含边界），且
AB
•
AC
=2
3
，∠BAC=30°，若△MBC，△MCA和△MAB的面积分别为x，y，z．
（1）x+y+z=
 
；
（2）定义f（x，y，z）=
1
x
+
4
y
+
9
z
，则f（x，y，z）的最小值是
 
．
已知M是△ABC内一点，且
AB
•
AC
=2
3
，∠BAC=30°，若△MBC，△MAB，△MAC的面积分别为
1
2
，x，y，则
1
x
+
1
y
的最小值是
 
．
已知M是△ABC内的一点，且
AB
•
AC
=2
3
，∠BAC=30°，若△MBC，△MCA，△MAB的面积分别为
1
2
，x，y，则
1
x
+
4
y
的最小值为
 
．
已知M是△ABC内的一点，且
AB
•
AC
=2
3
，∠BAC=30°．定义：f（M）=（x，y，z），其中x，y，z分别为△MBC，△MCA，△MAB的面积，若f（M）=（x，y，
1
2
），则
1
2x
+
2
y
的最小值为
9
9
，此时f（M）=（
(
1
6
，
1
3
，
1
2
)
(
1
6
，
1
3
，
1
2
)
．
已知M是△ABC内的一点（不含边界），且
AB
.
AC
=2
3
∠BAC=30°，若△MBC，△MCA和△MAB的面积分别为x，y，z，则
1
x+y
+
4
z
的最小值是
9
9
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网