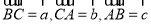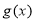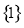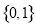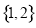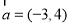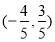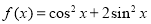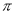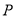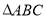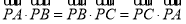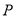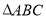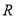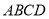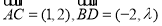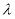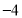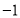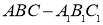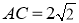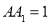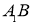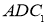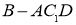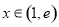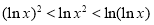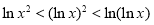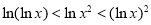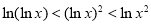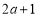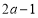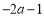题目内容
定义在 上的奇函数
上的奇函数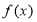 满足:当
满足:当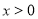 时,
时, ,则方程
,则方程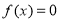 的实数根的个数是( )
的实数根的个数是( )
A. 1 B. 2 C. 3 D. 5
C
【解析】
试题分析:当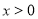 时,
时,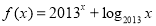 ,由指数函数与对数函数的图像与性质可知,此时函数
,由指数函数与对数函数的图像与性质可知,此时函数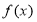 在
在 为增函数,而当
为增函数,而当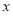 从
从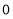 的右侧无限靠近
的右侧无限靠近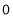 时,
时,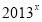 的值无限接近1,
的值无限接近1,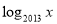 趋向负无穷大,当
趋向负无穷大,当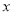 趋向正无穷大时,
趋向正无穷大时,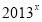 与
与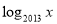 的值都趋向正无穷大值,所以
的值都趋向正无穷大值,所以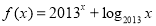 在
在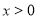 时有且只有一个零点;根据函数
时有且只有一个零点;根据函数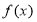 为
为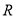 上的奇函数,故在
上的奇函数,故在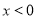 时,也有且只有一个零点,而
时,也有且只有一个零点,而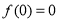 的,综上可知,函数
的,综上可知,函数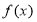 在
在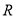 上有且只有三个零点,即方程
上有且只有三个零点,即方程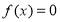 有且只有三个实数根,选C.
有且只有三个实数根,选C.
考点:1.函数的奇偶性;2.方程的解与函数的零点问题;3.指数函数与对数函数的图像与性质.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目