题目内容
对函数y=f(x)(x1≤x≤x2),设点A(x1,y1)、B(x2,y2)是图象上的两端点,O为坐标原点,且点N满足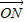 =
=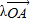 +(1-λ)
+(1-λ)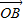 ,λ≥0,点M(x,y)在函数y=f(x)的图象上,且x=λx1+(1-λ)x2,则称|MN|的最大值为函数的“高度”,则函数f(x)=x2-2x-1在区间[-1,3]上的“高度”为 .
,λ≥0,点M(x,y)在函数y=f(x)的图象上,且x=λx1+(1-λ)x2,则称|MN|的最大值为函数的“高度”,则函数f(x)=x2-2x-1在区间[-1,3]上的“高度”为 .
【答案】分析:利用向量共线即可得出点N的坐标及λ的取值范围、利用两点间的距离公式即可得出|MN|、再二次函数的单调性即可得出.
解答:解:由函数f(x)=x2-2x-1及区间[-1,3]可得区间端点A(-1,2),B(3,2).
∴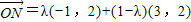 =(3-4λ,2),∴N(3-4λ,2);
=(3-4λ,2),∴N(3-4λ,2);
∵点N满足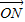 =
=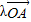 +(1-λ)
+(1-λ)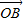 ,λ≥0,∴0≤λ≤1.
,λ≥0,∴0≤λ≤1.
∴xM=3-4λ,yM=(3-4λ)2-2(3-4λ)-1=16λ2-16λ+2,
∴|MN|=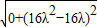 =|16λ2-16λ|=
=|16λ2-16λ|=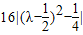 ,
,
∵λ∈[0,1],∴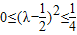 ,
,
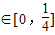 ,
,
∴|MN|≤4.
∴函数f(x)=x2-2x-1在区间[-1,3]上的“高度”为4.
故答案为4.
点评:正确理解新定义、向量共线、二次函数的单调性是解题的关键.
解答:解:由函数f(x)=x2-2x-1及区间[-1,3]可得区间端点A(-1,2),B(3,2).
∴
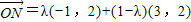 =(3-4λ,2),∴N(3-4λ,2);
=(3-4λ,2),∴N(3-4λ,2);∵点N满足
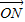 =
=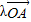 +(1-λ)
+(1-λ)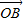 ,λ≥0,∴0≤λ≤1.
,λ≥0,∴0≤λ≤1.∴xM=3-4λ,yM=(3-4λ)2-2(3-4λ)-1=16λ2-16λ+2,
∴|MN|=
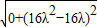 =|16λ2-16λ|=
=|16λ2-16λ|=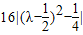 ,
,∵λ∈[0,1],∴
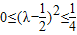 ,
,
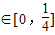 ,
,∴|MN|≤4.
∴函数f(x)=x2-2x-1在区间[-1,3]上的“高度”为4.
故答案为4.
点评:正确理解新定义、向量共线、二次函数的单调性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目