题目内容
一个空间四边形ABCD的四条边及对角线AC的长均为
,二面角D-AC-B的余弦值为
,则下列论断正确的是( )
| 2 |
| 1 |
| 3 |
| A、空间四边形ABCD的四个顶点在同一球面上且此球的表面积为3π | ||
| B、空间四边形ABCD的四个顶点在同一球面上且此球的表面积为4π | ||
C、空间四边形ABCD的四个顶点在同一球上且此球的表面积为3
| ||
| D、不存在这样的球使得空间四边形ABCD的四个顶点在此球面上 |
分析:由题意,求出BD的长,然后判断空间四边形ABCD的四个顶点是否在同一球面上,求出球的表面积即可.
解答: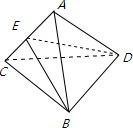 解:如图AC=AB=AD=BC=CD=
解:如图AC=AB=AD=BC=CD=
,cos∠DEB=
,
E为AC的中点,EB=ED=
,
所以BD2=2BE2-2×
×BE2
BD=
ABCD的几何体为正四面体,有外接球,球的半径为:
球的表面积为:3π
故选A
 解:如图AC=AB=AD=BC=CD=
解:如图AC=AB=AD=BC=CD=| 2 |
| 1 |
| 3 |
E为AC的中点,EB=ED=
| ||
| 2 |
所以BD2=2BE2-2×
| 1 |
| 3 |
BD=
| 2 |
ABCD的几何体为正四面体,有外接球,球的半径为:
| ||
| 2 |
球的表面积为:3π
故选A
点评:本题是基础题,考查二面角的求法,几何体的外接球的判断,以及外接球的表面积的求法,考查逻辑推理能力,计算能力,是好题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目