题目内容
记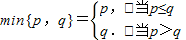
．若函数
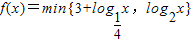，用分段函数形式写出函数f（x）的解析式，并求f（x）＜2的解集．
【答案】分析：根据题意，min{p，q}表示两个数中较小的数，比较两个数的大小可进行做差比较，欲求f（x）＜2的解集需要分段求解，分别求出在每一段上的解集，然后求它们的并集．
解答：解：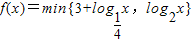
=
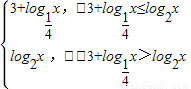
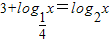得x=4．又函数
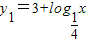在（0，+∞）内递减，y2=log2x在（0，+∞）内递增，所以当0＜x＜4时，
；当x≥4时，
．
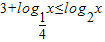所以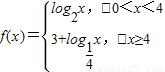
．
f（x）＜2等价于：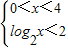
①或
②．
解得：0＜x＜4或x＞4，
故f（x）＜2的解集为（0，4）∪（4，+∞）．
点评：本题考查了函数与方程的综合运用，以及解不等式的解集．
解答：解：
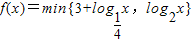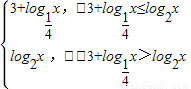
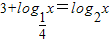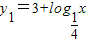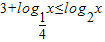=得x=4．又函数在（0，+∞）内递减，y2=log2x在（0，+∞）内递增，所以当0＜x＜4时，；当x≥4时，．所以
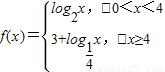．f（x）＜2等价于：
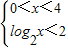①或②．解得：0＜x＜4或x＞4，
故f（x）＜2的解集为（0，4）∪（4，+∞）．
点评：本题考查了函数与方程的综合运用，以及解不等式的解集．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
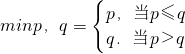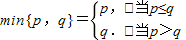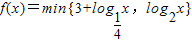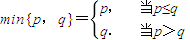．若函数
，
．若函数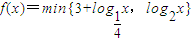
，
．若函数
，
．若函数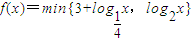
，