题目内容
设函数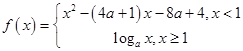
(1)当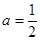 时,求函数
时,求函数 的值域;
的值域;
(2)若函数 是(-
是(- ,+
,+ )上的减函数,求实数
)上的减函数,求实数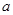 的网取值范围.
的网取值范围.
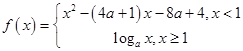
(1)当
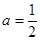 时,求函数
时,求函数 的值域;
的值域;(2)若函数
 是(-
是(-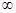 ,+
,+ )上的减函数,求实数
)上的减函数,求实数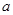 的网取值范围.
的网取值范围.(1)R(2)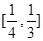
试题分析:(Ⅰ)
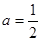 时,
时, 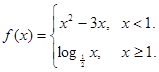
当
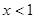 时,
时,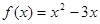 是减函数,所以
是减函数,所以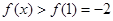
即
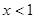 时,
时,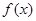 的值域是
的值域是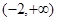 . 3 分
. 3 分当
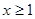 时,
时,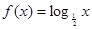 是减函数,所以
是减函数,所以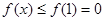
即
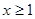 时,
时,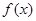 的值域是
的值域是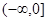 5 分
5 分于是函数
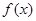 的值域是
的值域是 6分
6分(Ⅱ) 若函数
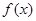 是(-
是(-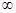 ,+
,+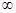 )上的减函数,则下列①②③三个条件同时成立:
)上的减函数,则下列①②③三个条件同时成立:①
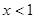 ,
,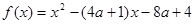 是减函数, 于是
是减函数, 于是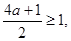 则
则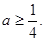
8分
②
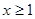 时,
时,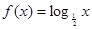 是减函数,则
是减函数,则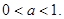 10 分
10 分③
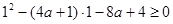 ,则
,则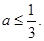 11 分
11 分于是实数
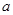 的取值范围是
的取值范围是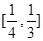 . ………….. 12 分
. ………….. 12 分点评:分段函数值域是各段函数值的范围的并集,第二问中函数在R上递减需满足各段递减且相邻的两段之间也是递减的,本题中的第三个条件在解题中容易忽略

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
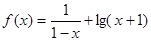 的定义域是
的定义域是 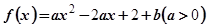 在区间
在区间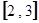 上的值域为
上的值域为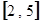
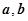 的值;
的值;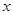 的函数
的函数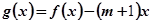 在区间
在区间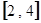 上为单调函数,求实数
上为单调函数,求实数 的取值范围.
的取值范围. 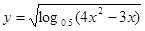 的定义域为
的定义域为 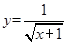 的定义域是( )
的定义域是( )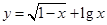 的定义域为 .
的定义域为 .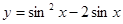 的值域是
的值域是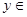 ;
;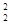 x+log2x2+2的值域是( )
x+log2x2+2的值域是( )