题目内容
如果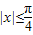
，那么函数f（x）=cos2x+sinx的最小值是 ．
【答案】分析：利用三角函数的平方关系式，化简函数的表达式，结合x的范围，求出sinx的范围，然后求出函数的最小值．
解答：解：函数f（x）=cos2x+sinx=1-sin2x+sinx=-（sinx-
）2+
，
因为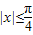
，所以sinx∈
，
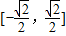当sinx=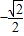
时，函数取得最小值：
．
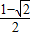故答案为：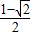
．
点评：本题是中档题，考查三角函数的化简求值，考查计算能力转化思想，常考题型．
解答：解：函数f（x）=cos2x+sinx=1-sin2x+sinx=-（sinx-
）2+，因为
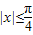，所以sinx∈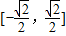，当sinx=
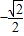时，函数取得最小值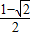：．故答案为：
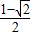．点评：本题是中档题，考查三角函数的化简求值，考查计算能力转化思想，常考题型．
练习册系列答案
相关题目
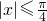，那么函数f（x）=cos2x+sinx的最小值是________．
，那么函数f（x）=cos2x+sinx的最小值是 ．