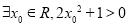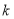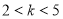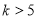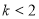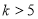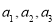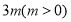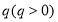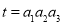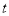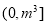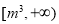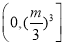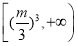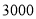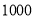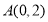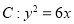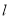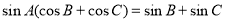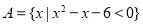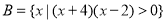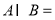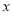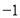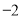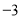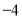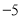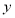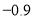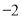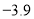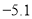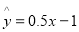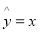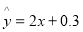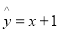题目内容
已知函数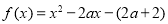 .
.
(1)解关于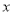 的不等式
的不等式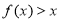 ;
;
(2)若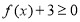 在区间
在区间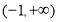 上恒成立,求实数
上恒成立,求实数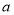 的取值范围.
的取值范围.
(1)当 时,原不等式的解集为
时,原不等式的解集为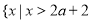 或
或 ;当
;当 时,解集为
时,解集为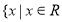 且
且 ;当
;当 时,解集为
时,解集为 或
或 ;(2)
;(2)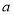 的取值范围是
的取值范围是 .
.
【解析】
试题分析:(1)本小题是含参数 的一元二次不等式问题,求解时先考虑因式分解,后针对根的大小进行分类讨论,分别写出不等式的解集即可;(2)不等式的恒成立问题,一般转化为函数的最值问题,不等式
的一元二次不等式问题,求解时先考虑因式分解,后针对根的大小进行分类讨论,分别写出不等式的解集即可;(2)不等式的恒成立问题,一般转化为函数的最值问题,不等式 即
即 在
在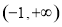 上恒成立可转化为
上恒成立可转化为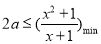 (
(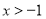 ),而函数
),而函数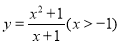 的最小值可通过均值不等式进行求解,从而可求得
的最小值可通过均值不等式进行求解,从而可求得 的取值范围.
的取值范围.
试题解析:(1)由 得
得 ,即
,即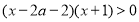 1分
1分
当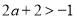 ,即
,即 时,原不等式的解为
时,原不等式的解为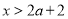 或
或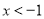 3分
3分
当 ,即
,即 时,原不等式的解为
时,原不等式的解为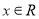 且
且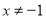 4分
4分
当 ,即
,即 时,原不等式的解为
时,原不等式的解为 或
或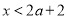
综上,当 时,原不等式的解集为
时,原不等式的解集为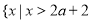 或
或 ;当
;当 时,解集为
时,解集为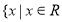 且
且 ;当
;当 时,解集为
时,解集为 或
或 6分
6分
(2)由 得
得 在
在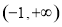 上恒成立,即
上恒成立,即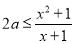 在
在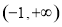 上恒成立,所以
上恒成立,所以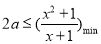 (
(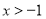 ) 8 分
) 8 分
令 ,则
,则 10分
10分
当且仅当 等号成立
等号成立


 ,即
,即
故实数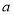 的取值范围是
的取值范围是 12分.
12分.
考点:1.一元二次含参不等式;2.分类讨论的思想;3.分离参数法;4.均值不等式.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目