题目内容

【题目】已知正项数列的前项和为，数列是首项为，公比为的等比数列．

（1）求证：数列是等差数列．

（2）若的前项和．

（3）在（2）条件下，是否存在常数，使得数列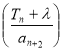为等比数列？若存在，试求出；若不存在，说明理由．

【答案】（1）详见解析（2）（3）

【解析】

试题分析：（1）由可求得数列的递推公式，从而得到数列为等差数列；（2）由已知求得的通项公式，进而得到，结合特点采用错位相减法求和；（3）整理数列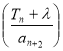通项公式，从而得到

试题解析：（1）由 ①

当， 解得 1分

当 ②

①-②得 2分

即 3分

因为，所以即

所以数列是以为首项为公差的等差数列 4分

（2）依题意

所以 5分

6分

①

, ② 7分

①—②得

9分

（3）因为 10分

所以要使数列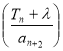为等比数列，当且仅当时

故存在，使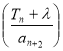为等比数列 12分

练习册系列答案
相关题目

【题目】用随机数表法进行抽样有以下几个步骤:①将总体中的个体编号;②获取样本号码;③选定开始的数字,这些步骤的先后顺序应为　(　　)

A. ①②③ B. ③②①

C. ①③② D. ③①②

【题目】已知曲线C上任意一点M满足|MF1|+|MF2|=4，其中F1（，F2（，

（Ⅰ）求曲线C的方程；

（Ⅱ）已知直线与曲线C交于A，B两点，是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O？若存在，求出k的值；若不存在，请说明理由．

【题目】如图，在四棱锥中，底面为正方形，平面，已知，为线段的中点.

（Ⅰ）求证：平面；

（Ⅱ）求平面与平面夹角的余弦值.

【题目】试编写程序确定S=1+4+7+10+…中至少加到第几项时S≥300.

【题目】算法程序如下:

a=input(“a=”);

b=input(“b=”);

c=input(“c=”);

if a

a=b;

end

if a

a=c;

end

print a;

该程序的功能是(　　)

A. 求出a,b,c三数中的最大数

B. 求出a,b,c三数中的最小数

C. 将a,b,c按从小到大排列

D. 将a,b,c按从大到小排列

【题目】设计一个程序将全班60名学生考试及格者的平均分计算并打印出来.

【题目】下列说法正确的是（ ）

A. 三点确定一个平面 B. 四边形一定是平面图形

C. 共点的三条直线确定一个平面 D. 梯形一定是平面图形

【题目】下列语句中是命题的有(　　)

①空集是任何集合的真子集.

②3x-2>0.

③垂直于同一条直线的两条直线必平行吗?

④把门关上.

A. 1个 B. 2个 C. 3个 D. 4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网