题目内容
已知函数f (x)的定义域为R,且f(x+2)-f(x+1)+f(x)=0,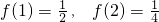 ,则f (2006)=________.
,则f (2006)=________.

分析:由f(x+2)=f(x+1)-f(x),知f(x+3)=f(x+2)-f(x+1),故f(x+2)+f(x+3)=f(x+1)-f(x)+f(x+2)-f(x+1),-f(x+3)=f(x),所以f(x+6)=f(x),所以周期T=6.由此能求出f(2006).
解答:∵f(x+2)=f(x+1)-f(x),
∴f(x+3)=f(x+2)-f(x+1),
∴f(x+2)+f(x+3)=f(x+1)-f(x)+f(x+2)-f(x+1),
∴f(x+3)=-f(x),
则-f(x+3)=f(x),
所以f(x+6)
=f[(x+3)+3]
=-f(x+3)
=f(x)
所以周期T=6.
∵2006÷6余数是2,
所以f(2006)=f(2)=
 .
.故答案为:
 .
.点评:本题考查函数的周期性的求法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为( )
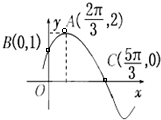

A、f(x)=2sin(
| ||||
B、f(x)=
| ||||
C、f(x)=2sin(
| ||||
D、f(x)=
|
 已知函数f(x)的定义域为[-1,5],部分对应值如下表.
已知函数f(x)的定义域为[-1,5],部分对应值如下表.
 已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则
已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则