题目内容
正三棱锥底面边长为a,侧棱与底面成角为60°,过底面一边作一截面使其与底面成30°的二面角,则此截面的面积为
.
| 3 |
| 8 |
| 3 |
| 8 |
分析:由于此题为正三棱锥且已知底面边长为a,作出顶点S在底面内的投影点O,由于为正三棱锥,所以S在底面内的投影点为三角形ABC的中心,连接SO,取边AB的中点,利用二面角的定义可以求出∠DEC即为二面角的平面角,∠DEC=60°即为侧棱与底面成角且值为60°,利用三角形的面积公式即可求出.
解答:解:∵三棱锥S-ABC底面△ABC边长为a,
侧棱与底面成角为60°,
过底面一边作一截面使其与底面成30°的二面角,
∴如图,E为AB中点,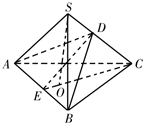
CE=
BC=
a,
∠DEC=30°,∠DCE=60°,
∴∠EDC=90°,
∴DE=CE•sin60°=
a•
=
a,
∴S△ADB=
•a•
a=
a2.
故答案为
a2.
侧棱与底面成角为60°,
过底面一边作一截面使其与底面成30°的二面角,
∴如图,E为AB中点,

CE=
| ||
| 2 |
| ||
| 2 |
∠DEC=30°,∠DCE=60°,
∴∠EDC=90°,
∴DE=CE•sin60°=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
∴S△ADB=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
故答案为
| 3 |
| 8 |
点评:此题中点考查了学生的空间想象能力,还考查了三棱锥的定义及在三角形中利用边角关系求解三角形,还考查了线面角与二面角的定义及学生的计算三角形的计算能力.本题综合性强,难度大,易出错,解题时要认真审题,仔细解答.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 正三棱锥底面边长为a,侧棱与底面成角为60°,过底面一边作一截面使其与底面成30°的二面角,则此截面的面积为( )
正三棱锥底面边长为a,侧棱与底面成角为60°,过底面一边作一截面使其与底面成30°的二面角,则此截面的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 a2 B.
a2 B. a2 C.
a2 C. a2 D.
a2 D.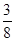 a2
a2
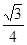 a2
D.
a2
D. 
