Question

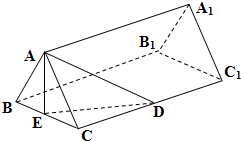（2009•惠州模拟）如图，已知正三棱柱ABC-A₁B₁C₁的底面边长是2，D、E是CC₁、BC的中点，AE=DE
（1）求此正三棱柱的侧棱长；  
（2）正三棱柱ABC-A₁B₁C₁表面积．

Answer 1

分析：（1）设正三棱柱ABC-A₁B₁C₁的侧棱长为x，取BC中点E，连结AE．在Rt△AED中列出关于x的方程求解
（2）根据棱柱的表面积和体积公式计算即可．

解答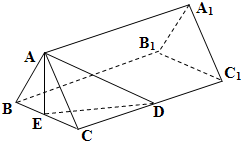：解：（1）设正三棱柱ABC-A₁B₁C₁的侧棱长为x，
取BC中点E，连结AE．
∵△ABC是正三角形，
∴AE⊥BC．…（2分）
又底面ABC⊥侧面BB₁C₁C，且交线为BC，
∴AE⊥侧面BB₁C₁C．连结ED，
在Rt△AED中，由AE=DE，得

1+ x2 4

=

3

，…（4分）
解得x=2

2

…（6分）
（2）S=S_侧+S_底…（8分）

S侧=3×2×2 2 =12 2 S底=2× 3 4 ×22=2 3

…（12分）
∴S=S侧+S底=12

2

+2

3

．…（14分）

点评：本题考查空间几何体的表面积和体积，要具备空间想象能力、计算能力．