题目内容
以下四个命题:
①x=1是函数f(x)=(x2-1)3+2的极值点;
②当h无限趋近于0时,
无限趋近于
;
③?q是?p的必要不充分条件,则p是q的充分不必要条件;
④已知a,b,c均为实数,b2-4ac>0是ax2+bx+c>0的必要不充分条件.
其中真命题的序号为 (写出所有真命题的序号).
①x=1是函数f(x)=(x2-1)3+2的极值点;
②当h无限趋近于0时,
| ||||
| 2h |
| ||
| 12 |
③?q是?p的必要不充分条件,则p是q的充分不必要条件;
④已知a,b,c均为实数,b2-4ac>0是ax2+bx+c>0的必要不充分条件.
其中真命题的序号为
分析:针对每一个选支进行逐一进行判定,①用极值的定义进行判定,②利用导数的定义进行判定,③用逆否命题的等价性进行判定,④利用恒成立转化成图象恒在x轴上方进行判定.
解答:解:①f′(x)=6x(x2-1)2,当x∈(0,1)时f′(x)>0
x∈(1,+∞)时f′(x)>0,所以在x=1处不是函数的极值,故不正确
②正确,
③?q是?p的必要不充分条件则?q??p,所以p⇒q,
p是q的充分不必要条件;正确
④ax2+bx+c>0⇒b2-4ac>0,a>0,b2-4ac>0是ax2+bx+c>0的必要不充分条件,命题正确
故答案为②③④
x∈(1,+∞)时f′(x)>0,所以在x=1处不是函数的极值,故不正确
②正确,
③?q是?p的必要不充分条件则?q??p,所以p⇒q,
p是q的充分不必要条件;正确
④ax2+bx+c>0⇒b2-4ac>0,a>0,b2-4ac>0是ax2+bx+c>0的必要不充分条件,命题正确
故答案为②③④
点评:本题主要考查了利用导数研究函数的极值,以及充分条件、必要条件和充要条件的判断,属于基础题.

练习册系列答案
相关题目
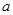 无限趋近于0时,
无限趋近于0时,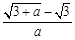 无限趋近于
无限趋近于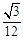 ;
;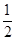 ”的必要不充分。
”的必要不充分。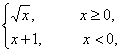 则
则