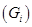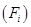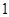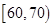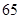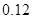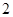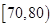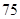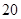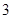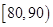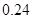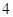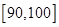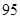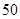题目内容
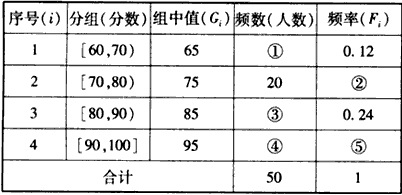
为了让学生更多地了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据下面的频率分布表,解答下列问题:| 序号 (i) |
分组 (分数) |
本组中间值 (Gi) |
频数 (人数) |
频率 (Fi) |
| 1 | (60,70) | 65 | ① | 0.12 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.24 |
| 4 | [90,100] | 95 | ④ | ⑤ |
| 合 计 | 50 | 1 | ||
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在参赛的800名学生中大概有多少同学获奖?
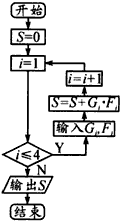
(3)请根据频率分布表估计该校高二年级参赛的800名同学的平均成绩.
分析:(1)由已知中频率分布表,样本容量为50,根据频率=频数÷样本容量,即可求出频率分布表中的空格中的值;
(2)根据(1)中数据,求出成绩不低于85分的同学的频率,再由总体容量为800,即可估算出参赛的800名学生中大概有多少同学获奖;
(3)平均成绩的估算值,等于各组组中值与该组频率乘积的累加值,代入计算后,即可得到答案.
(2)根据(1)中数据,求出成绩不低于85分的同学的频率,再由总体容量为800,即可估算出参赛的800名学生中大概有多少同学获奖;
(3)平均成绩的估算值,等于各组组中值与该组频率乘积的累加值,代入计算后,即可得到答案.
解答:解:(1)①为6,②为0.4,③为12,④为12⑤为0.24.(5分)
(2)(
×0.24+0.24)×800=288,
即在参加的800名学生中大概有288名同学获奖.(9分)
(3)65×0.12+75×0.4+85×0.24+95×0.24=81(4)
估计平均成绩为81分.(12分)
(2)(
| 1 |
| 2 |
即在参加的800名学生中大概有288名同学获奖.(9分)
(3)65×0.12+75×0.4+85×0.24+95×0.24=81(4)
估计平均成绩为81分.(12分)
点评:本题考查的知识点是用样本的频分布估计总体分布,根据频率分布表计算数据的平均数,其中频率=频数÷样本容量,平均成绩的估算值,等于各组组中值与该组频率乘积的累加值,这两个公式是解答本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
(本小题满分12分)
为了让学生更多地了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有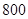 名学生参加了这次竞赛。为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为
名学生参加了这次竞赛。为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为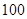 分)进行统计。请你根据下面的频率分布表,解答下列问题:
分)进行统计。请你根据下面的频率分布表,解答下列问题:
|
序号 ( |
分组 (分数) |
本组中间值
|
频数 (人数) |
频率
|
|
|
|
|
①[] |
|
|
|
|
|
|
②] |
|
|
|
|
③ |
|
|
|
|
|
④ |
⑤ |
|
合 计 |
|
|
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于 分的同学能获奖,请估计在参赛的
分的同学能获奖,请估计在参赛的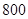 名学生中大概有多少同学获奖?
名学生中大概有多少同学获奖?
|
为了让学生更多地了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据下面的频率分布表,解答下列问题:
| 序号 (i) | 分组 (分数) | 本组中间值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | (60,70) | 65 | ① | 0.12 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.24 |
| 4 | [90,100] | 95 | ④ | ⑤ |
| 合 计 | 50 | 1 | ||
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在参赛的800名学生中大概有多少同学获奖?
(3)请根据频率分布表估计该校高二年级参赛的800名同学的平均成绩.
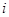 )
)