题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,点
,点![]() ,
,![]() ,点
,点![]() 在圆
在圆![]() 上,
上,![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 轴上方),点
轴上方),点![]() 是抛物线
是抛物线![]() 上的动点,点
上的动点,点![]() 为
为![]() 的外心,求线段
的外心,求线段![]() 长度的最大值,并求出当线段
长度的最大值,并求出当线段![]() 长度最大时,
长度最大时,![]() 外接圆的标准方程.
外接圆的标准方程.
【答案】(1)![]() (2)
(2)![]() 的最大值为
的最大值为![]() ;
;![]()
【解析】
(1)设![]() ,根据
,根据![]() 得到
得到![]() ,转化为坐标表示,得到
,转化为坐标表示,得到![]() ,即
,即![]() ,从而得到圆
,从而得到圆![]() 的方程;
的方程;
(2)由![]() 得到
得到![]() 、
、![]() 的坐标,表示出线段
的坐标,表示出线段![]() 的中垂线
的中垂线![]() ,令
,令![]() ,得到
,得到![]() 的外心
的外心![]() 的坐标,由
的坐标,由![]() 在抛物线
在抛物线![]() 上得
上得![]() ,从而得到
,从而得到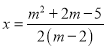 ,再由基本不等式,得到其最大值,确定出
,再由基本不等式,得到其最大值,确定出![]() 点坐标,再求出
点坐标,再求出![]() 外接圆的半径,得到所求圆的方程.
外接圆的半径,得到所求圆的方程.
解:(1)设![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]()
所以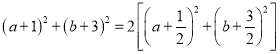 ,
,
由上式得:![]() ,所以
,所以![]() ,所以圆
,所以圆![]() 的方程为
的方程为![]() .
.
(2)把![]() 代入圆
代入圆![]() 的方程得
的方程得![]() ,所以
,所以![]() ,
,![]() ,
,
作出线段![]() 的中垂线
的中垂线![]() ,则
,则![]() 的外心
的外心![]() 为直线
为直线![]() 与
与![]() 轴的交点.
轴的交点.
直线![]() 的方程为:
的方程为:![]() .
.
当![]() 时,
时,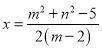 .
.
因为点![]() 在抛物线
在抛物线![]() 上,所以
上,所以![]()
所以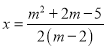 .
.
由![]() 得
得 ,
,
所以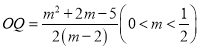 ,
,
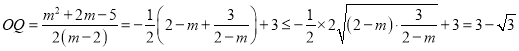 .
.
当且仅当![]() 时,即
时,即![]() 时
时![]() 取到最大值
取到最大值![]() .
.
此时![]() 点坐标为
点坐标为![]() ,所以
,所以![]() 外接圆的半径
外接圆的半径![]() ,
,
所以![]() 外接圆的标准方程为
外接圆的标准方程为![]() .
.

 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】为了增强学生的环境意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理,制成下表:
成绩 |
|
|
|
|
|
|
频数 | 2 | 3 | 14 | 15 | 14 | 4 |
(1)作出被抽查学生成绩的频率分布直方图;
(2)若从成绩在![]() 中选一名学生,从成绩在
中选一名学生,从成绩在![]() 中选出2名学生,共3名学生召开座谈会,求
中选出2名学生,共3名学生召开座谈会,求![]() 组中学生
组中学生![]() 和
和![]() 组中学生
组中学生![]() 同时被选中的概率?
同时被选中的概率?
【题目】某市实验中学数学教研组,在高三理科一班进行了一次“采用两种不同方式进行答卷”的考试实验,第一种做卷方式:按从前往后的顺序依次做;第二种做卷方式:先做简单题,再做难题.为了比较这两种做卷方式的效率,选取了![]() 名学生,将他们随机分成两组,每组
名学生,将他们随机分成两组,每组![]() 人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
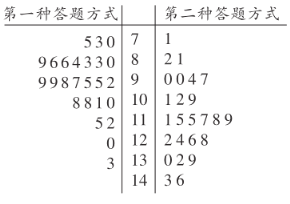
![]() 若
若![]() 分(含
分(含![]() 分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
![]() 设
设![]() 名学生考试分数的中位数为
名学生考试分数的中位数为![]() ,根据茎叶图填写下面的
,根据茎叶图填写下面的![]() 列联表:
列联表:
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 | |||
第一种做卷方式 | |||
合计 |
根据列联表,能否有![]() 的把握认为两种做卷方式的效率有差异?
的把握认为两种做卷方式的效率有差异?
附: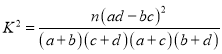 ,
,![]() .
.
|
|
|
|
|
|
|
|