Question

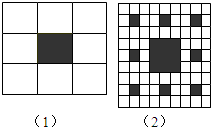一个正方形被等分成九个相等的小正方形，将中间的一个正方形挖掉如图（1）；再将剩余的每个正方形都分成九个相等的小正方形，并将中间一个挖掉，得图（2）；如此继续下去…
（1）第三个图中共挖掉多少个正方形；
（2）设原正方形边长为1，则第n个图中被挖掉的所有小正方形的面积和为多少？

Answer 1

分析：（1）通过研究前后两个图形挖去正方形个数的变化规律，从而求出答案；
（2）第图（1）到第图n被挖掉的正方形的边长及个数分别组成等比数列{a_n}，由此可求第n个图中被挖掉的所有小正方形的面积和．

解答：解：（1）由题意，第三个图中共挖掉1+8+8²=73个正方形；
（2）第图（1）到第图n被挖掉的正方形的边长组成等比数列{a_n}，且a_n=(

1

3

)n，
其个数组成等比数列{b_n}，且b_n=(

1

8

)n-1
∴第n个图中被挖掉的所有小正方形的面积和为S=

1

9

+

8

92

+…+

8n-1

9n

=1-(

8

9

)n

点评：本题主要考查图形规律下的数列问题，关键是寻找规律，转化为运用数列知识求解．