题目内容
已知集合A={x|x=a0+a1×3+a2×32+a3×33},其中ak∈{0,1,2}(k=0,1,2,3),且a3≠0,则A中所有元素之和等于( )
| A.3 240 | B.3 120 |
| C.2 997 | D.2 889 |
D
解析

练习册系列答案
相关题目
若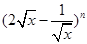 展开式中所有项的二项式系数之和为64,则展开式中含
展开式中所有项的二项式系数之和为64,则展开式中含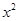 项的系数是( )
项的系数是( )
| A.192 | B.182 | C.-192 | D.-182 |
已知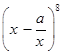 展开式中常数项为5670,其中
展开式中常数项为5670,其中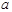 是常数,则展开式中各项系数的和是( )
是常数,则展开式中各项系数的和是( )
| A.28 | B.48 | C.28或48 | D.1或28 |
若 展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
A. | B.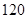 | C.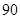 | D.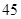 |
若(3x+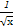 )n的展开式中各项系数的和为1024,则展开式中含x的整数次幂的项共有( )
)n的展开式中各项系数的和为1024,则展开式中含x的整数次幂的项共有( )
| A.2项 | B.3项 | C.5项 | D.6项 |
将字母a,a,b,b,c,c排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有( )
| A.12种 | B.18种 | C.24种 | D.36种 |
我们把各位数字之和为6的四位数称为“六合数”(如2 013是“六合数”),则“六合数”中首位为2的“六合数”共有( )
| A.18个 | B.15个 |
| C.12个 | D.9个 |
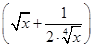 n的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )
n的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )