题目内容
已知函数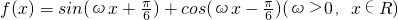 ,且该函数图象相邻两对称轴间的距离为
,且该函数图象相邻两对称轴间的距离为 .
.
(I)求函数f(x)的解析式;
(II)若不等式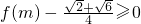 成立,求实数m的取值范围.
成立,求实数m的取值范围.
解:(I)∵函数 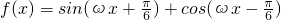 =
= sinωx+
sinωx+ cosωx+
cosωx+ cosωx+
cosωx+ sinωx
sinωx
= (sinωx+cosωx)=
(sinωx+cosωx)=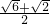 sin(ωx+
sin(ωx+ ).
).
∵该函数图象相邻两对称轴间的距离为 ,∴函数f(x)的最小正周期为π,
,∴函数f(x)的最小正周期为π,
即 =π,ω=2,f(x)=
=π,ω=2,f(x)=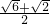 sin(2x+
sin(2x+ ).
).
(II)∵不等式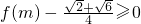 成立,∴
成立,∴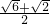 sin(2m+
sin(2m+ )≥
)≥ ,
,
∵sin(2x+ )≥
)≥ .
.
∴2kπ- ≤2m+
≤2m+ )≤2kπ+
)≤2kπ+ ,k∈z.解得 kπ-
,k∈z.解得 kπ-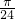 ≤m≤kπ+
≤m≤kπ+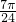 ,k∈z.
,k∈z.
故实数m的取值范围为[kπ-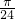 ,kπ+
,kπ+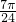 ]k∈z.
]k∈z.
分析:(I)化简函数f(x)的解析式为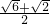 sin(ωx+
sin(ωx+ ),由该函数图象相邻两对称轴间的距离为
),由该函数图象相邻两对称轴间的距离为 ,可得函数f(x)的最小正周期为π,由此求得ω=2.
,可得函数f(x)的最小正周期为π,由此求得ω=2.
(II)由不等式可得sin(2x+ )≥
)≥ ,故有 2kπ-
,故有 2kπ- ≤2m+
≤2m+ )≤2kπ+
)≤2kπ+ ,k∈z.由此解得实数m的取值范围.
,k∈z.由此解得实数m的取值范围.
点评:本题主要考查三角函数的恒等变换及化简求值,复合函数的单调性,解三角不等式,属于中档题.
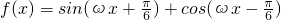 =
= sinωx+
sinωx+ cosωx+
cosωx+ cosωx+
cosωx+ sinωx
sinωx=
 (sinωx+cosωx)=
(sinωx+cosωx)=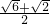 sin(ωx+
sin(ωx+ ).
).∵该函数图象相邻两对称轴间的距离为
 ,∴函数f(x)的最小正周期为π,
,∴函数f(x)的最小正周期为π,即
 =π,ω=2,f(x)=
=π,ω=2,f(x)=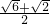 sin(2x+
sin(2x+ ).
).(II)∵不等式
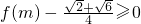 成立,∴
成立,∴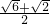 sin(2m+
sin(2m+ )≥
)≥ ,
,∵sin(2x+
 )≥
)≥ .
.∴2kπ-
 ≤2m+
≤2m+ )≤2kπ+
)≤2kπ+ ,k∈z.解得 kπ-
,k∈z.解得 kπ-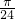 ≤m≤kπ+
≤m≤kπ+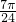 ,k∈z.
,k∈z.故实数m的取值范围为[kπ-
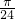 ,kπ+
,kπ+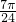 ]k∈z.
]k∈z.分析:(I)化简函数f(x)的解析式为
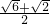 sin(ωx+
sin(ωx+ ),由该函数图象相邻两对称轴间的距离为
),由该函数图象相邻两对称轴间的距离为 ,可得函数f(x)的最小正周期为π,由此求得ω=2.
,可得函数f(x)的最小正周期为π,由此求得ω=2.(II)由不等式可得sin(2x+
 )≥
)≥ ,故有 2kπ-
,故有 2kπ- ≤2m+
≤2m+ )≤2kπ+
)≤2kπ+ ,k∈z.由此解得实数m的取值范围.
,k∈z.由此解得实数m的取值范围.点评:本题主要考查三角函数的恒等变换及化简求值,复合函数的单调性,解三角不等式,属于中档题.

练习册系列答案
相关题目
 =(sin(ωx+?),2),
=(sin(ωx+?),2), =(1,cos(ωx+?))
=(1,cos(ωx+?))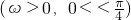 ,函数f(x)=(
,函数f(x)=(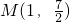 ,且该函数相邻两条对称轴间的距离为2.
,且该函数相邻两条对称轴间的距离为2.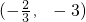 平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.
平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.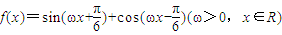 ,且该函数图象相邻两对称轴间的距离为
,且该函数图象相邻两对称轴间的距离为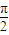 .
.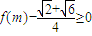 成立,求实数m的取值范围.
成立,求实数m的取值范围.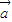 =(sin(ωx+ϕ),2),
=(sin(ωx+ϕ),2),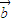 =(1,cos(ωx+ϕ))
=(1,cos(ωx+ϕ))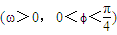 ,函数f(x)=(
,函数f(x)=(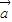 +
+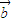 )•(
)•(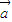 -
-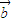 )的图象过点
)的图象过点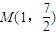 ,且该函数相邻两条对称轴间的距离为2.
,且该函数相邻两条对称轴间的距离为2.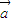 =
=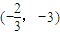 平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.
平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.