题目内容
甲、乙、丙三人玩游戏,规定每次在写有数字1,2,3,4,5,6的6张卡片中随机抽取一张,若数字为1或2或3,则甲得1分;若数字为4或5,则乙得1分;若数字为6,则丙得1分.一共抽取3次,得2分或3分者获胜.(Ⅰ)求乙获胜的概率;
(Ⅱ)记ξ为甲得的分数,求随机变量ξ的概率分布列和数学期望.
分析:(Ⅰ)乙获胜有下列三种情况:①乙3分;②乙2分,丙1分;③乙2分,甲1分.这三种情况是互斥的,根据独立重复试验的概率公式和互斥事件的概率公式得到结果.
(II)ξ为甲得的分数,ξ的取值可以为0,1,2,3,结合变量对应的事件,利用独立重复试验概率公式,写出变量对应的概率,写出分布列和期望值.
(II)ξ为甲得的分数,ξ的取值可以为0,1,2,3,结合变量对应的事件,利用独立重复试验概率公式,写出变量对应的概率,写出分布列和期望值.
解答:解:(Ⅰ)乙获胜有下列三种情况:①乙3分;②乙2分,丙1分;
③乙2分,甲1分.这三种情况是互斥的,
∴乙获胜的概率
P=(
)3+
×(
)2×
+
× (
)2×
=
.
(Ⅱ)ξ为甲得的分数,ξ的取值可以为0,1,2,3
∴P(ξ=3)=(
)3=
;
P=(ξ=2)
×(
)2×
+(
)2×
×
=
+
=
;
P=(ξ=1)
×(
)×
×(
)2×
+
(
)2×
=
;
P=(ξ=0)=(
)3×(
)3+
(
)2×
+
(
)2×
=
.
∴ξ的概率分布列:
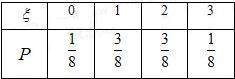
∴Eξ=
+2×
+3×
=
.
③乙2分,甲1分.这三种情况是互斥的,
∴乙获胜的概率
P=(
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| C | 2 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 7 |
| 27 |
(Ⅱ)ξ为甲得的分数,ξ的取值可以为0,1,2,3
∴P(ξ=3)=(
| 1 |
| 2 |
| 1 |
| 8 |
P=(ξ=2)
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 3 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 3 |
| 8 |
P=(ξ=1)
| A | 3 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| C | 3 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 3 |
| 8 |
P=(ξ=0)=(
| 1 |
| 6 |
| 1 |
| 3 |
| C | 3 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| C | 3 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 8 |
∴ξ的概率分布列:

∴Eξ=
| 3 |
| 8 |
| 3 |
| 8 |
| 1 |
| 8 |
| 3 |
| 2 |
点评:本题考查离散型随机变量的分布列和期望,考查独立重复试验,考查互斥事件的概率加法公式,是一个综合题目,这种题目可以作为高考卷中的解答题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目