Question

已知某射手射击一次，击中目标的概率是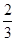．（1）求连续射击5次，恰有3次击中目标的概率；

（2）求连续射击5次，击中目标的次数X的数学期望和方差.

（3）假设连续2次未击中目标，则中止其射击，求恰好射击5次后，被中止射击的概率．（本题结果用分数表示即可）．

 

Answer 1

【答案】

解：（1）设“甲射击5次，恰有3次击中目标”为事件A，则．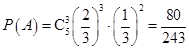

答：甲射击5次，恰有3次击中目标的概率为．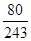     

（2）   ；

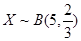
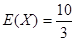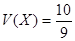
（3）方法1：设“甲恰好射击5次后，被中止射击”为事件C，由于甲恰好射击5次后被中止射击，所以必然是最后两次未击中目标，第三次击中目标，第一次与第二次至少有一次击中目标，则

．

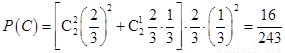答：甲恰好射击5次后，被中止射击的概率为．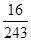       

方法2：设“甲恰好射击5次后，被中止射击”为事件C，由于甲恰好射击5次后被中止射击，所以必然是最后两次未击中目标，第三次击中目标，第一次与第二次至少有一次击中目标，则

．

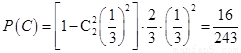答：甲恰好射击5次后，被中止射击的概率为．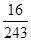

【解析】略