题目内容
定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”。现有定义在( )
(-∞,0)∪(0,+∞)上的如下函数:①f(x)=x²;②f(x)=2x;③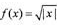 ;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
A.①② B.①③ C.③④ D.②④
【答案】
B
【解析】
试题分析:等比数列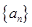 中,设公比为
中,设公比为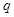 ,
,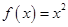 中
中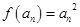
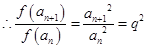 是等比数列,
是等比数列,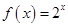 中
中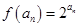
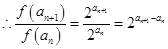
不是常数,不是等比数列,综上①为“保等比数列函数”②不是,结合选项可知选B
考点:等比数列的判定
点评:要判定一个数列是否为等比数列,通常利用定义:看相邻两项之比是否为常数

练习册系列答案
相关题目
若定义在(-1,0)内的函数f(x)=log2a(x+1)>0,则a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、(
| ||
| D、(0,+∞) |