题目内容
如图是一个正方体纸盒的展开图，在原正方体纸盒中有下列结论：①BM与ED平行；
②CN与BE是异面直线；
③CN与BM成60°角；
④DM与BN垂直．
其中，正确命题的序号是 ．
【答案】分析：先利用正方体纸盒的展开图，画出它的直观图，特别注意特殊点的位置，再在正方体中证明线线位置关系以及求异面直线所成的角即可
解答：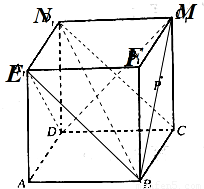
解：如图为正方体纸盒的直观图：
由图可知：BM与ED异面且垂直，①错误；
CN与BE平行，②错误；
异面直线CN与BM所成的角即∠EBM，由于△EBM为等边三角形，故∠EBM=60°，③正确；
因为DM⊥NC，DM⊥BC，NC∩BC=C，所以DM⊥平面NCB，所以DM⊥BN，④正确
故答案为③④
点评：本题考查了空间几何体的展开图与直观图间的关系，空间的线线位置关系及其证明，异面直线所成的角及其求法，将平面图准确的转化为直观图是解决本题的关键
解答：
解：如图为正方体纸盒的直观图：由图可知：BM与ED异面且垂直，①错误；
CN与BE平行，②错误；
异面直线CN与BM所成的角即∠EBM，由于△EBM为等边三角形，故∠EBM=60°，③正确；
因为DM⊥NC，DM⊥BC，NC∩BC=C，所以DM⊥平面NCB，所以DM⊥BN，④正确
故答案为③④
点评：本题考查了空间几何体的展开图与直观图间的关系，空间的线线位置关系及其证明，异面直线所成的角及其求法，将平面图准确的转化为直观图是解决本题的关键
练习册系列答案
相关题目
如图是一个正方体纸盒的展开图，在原正方体纸盒中有下列结论：
B.
C.
D.
如图是一个正方体纸盒的展开图，在原正方体纸盒中有下列结论：